题目内容

有5名学生和2名教师排成一排拍照，2名教师相邻但不排在两端，不同排法数共有（　　）
分析：先排5名学生方法有
A
5
5
种，再从5名学生形成的中间4个空中选出1个插入2名教师，方法有
A
1
4
•
A
2
2
 种，根据分步计数原理求得结果．
解答：解：第一步，先排5名学生方法有
A
5
5
种； 第二步，从5名学生形成的中间4个空中选出1个插入2名教师，方法有
A
1
4
•
A
2
2
 种，
再根据分步计数原理求得不同排法数共有
A
5
5
•
A
1
4
•
A
2
2
=960种，
故选C．
点评：本题主要考查排列组合、两个基本原理的实际应用，注意相邻问题用捆绑法，属于中档题．
练习册系列答案
相关题目
惠州市某校高三年级有男生720人，女生480人，教师80人，用分层抽样的方法从中抽取16人，进行问卷调查．设其中某项问题的选择支为“同意”和“不同意”两种，且每人都做了一种选择．下面表格中提供了被调查人答卷情况的部分信息．
同意 不同意 合计
男生 5
女生 4
教师 1
（1）请完成此统计表；
（2）试估计高三年级学生“同意”的人数；
（3）从被调查的女生中选取2人进行访谈，求选到的两名女生中，恰有一人“同意”一人“不同意”的概率．
某中学从高中三个年级选派2名教师和10名学生去外校考察学习，学生的名额分配如下：
高一年级 高二年级 高三年级
3人 5人 2人
（1）若从10名学生中选出2人做组长，求他们中恰好有1人是高二年级学生的概率；
（2）若将2名教师安排到三个年级（假设每名教师加入各年级是等可能的，且各位教师的选择是相互独立的），记安排到高二年级的教师人数为X，求随机变量X的分布列和数学期望．
为了解大学生观看某电视节目是否与性别有关，一所大学心理学教师从该校学生中随机抽取了50人进行问卷调查，得到了如下的列联表，若该教师采用分层抽样的方法从50份问卷调查中继续抽查了10份进行重点分析，知道其中喜欢看该节目的有6人
  喜欢看该节目 不喜欢看该节目 合计
女生   5  
男生 10    
合计     50
（Ⅰ） 请将上面的列联表补充完整；
（Ⅱ） 在犯错误的概率不超过0.005的情况下认为喜欢看该节目节目与性别是否有关？说明你的理由；
（ III） 已知喜欢看该节目的10位男生中，A1、A2、A3、A4、A5还喜欢看新闻，B1、B2、B3还喜欢看动画片，C1、C2还喜欢看韩剧，现再从喜欢看新闻、动画片和韩剧的男生中各选出1名进行其他方面的调查，求B1和C1不全被选中的概率．
下面的临界值表供参考：
P（K2≥K） 0.15 0.10 0.05 0.025 0.010 0.005 0.001
K 2.072 2.706 3.841 5.024 6.635 7.879 10.828
（参考公式：K2=
n(ad-bc)2
(a+b)(c+d)(a+c)(b+d)
，其中n=a+b+c+d）
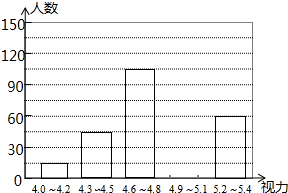精英家教网为进一步加强中小学生近视眼的防控工作，市教育局近期下发了有关文件，将学生视力保护工作纳入学校和教师的考核内容，为此，某县教育组管部门对今年初中毕业生的视力进行了一次抽样调查，并根据调查结果绘制如下频数分布表和频数分布直方图的一部分．
视力  频数（人） 频率
 4.0～4.2 15  0.05
 4.3～4.5 45  0.15
 4.6～4.8 105  0.35
 4.9～5.1 a  0.25
 5.2～5.4 60 b
请根据图表信息回答下列问题：
（1）求表中a、b的值，并将频数分布直方图补充完整；
（2）若视力在4.9以上（含4.9）均属正常，估计该县5600名初中毕业生视力正常的学生有多少人？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网