题目内容
已知抛物线C的参数方程为
(t为参数),设抛物线C的焦点为F,准线为l,P为抛物线上一点,PA⊥l,A为垂足,如果直线AF的斜率为-
,那么|PF|=______.
|
| 3 |
把抛物线C的参数方程
(t为参数),消去参数化为普通方程为 y2=8x.
故焦点F(2,0),准线方程为 x=-2,再由直线FA的斜率是-
,可得直线FA的倾斜角为120°,
设准线和x轴的交点为M,则∠AFM=60°,且MF=p=4,∴∠PAF=180°-120°=60°.
∴AM=MF•tan60°=4
,故点A(0,4
),把y=4
代入抛物线求得x=6,
∴点P(6,4
),
故|PF|=
=8,
故答案为 8.
|
故焦点F(2,0),准线方程为 x=-2,再由直线FA的斜率是-
| 3 |
设准线和x轴的交点为M,则∠AFM=60°,且MF=p=4,∴∠PAF=180°-120°=60°.
∴AM=MF•tan60°=4
| 3 |
| 3 |
| 3 |
∴点P(6,4
| 3 |
故|PF|=
(6-2)2+(4
|
故答案为 8.

练习册系列答案
相关题目
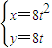 (t为参数),若斜率为1的直线经过抛物线C的焦点,且与圆(x-4)2+y2=r2(r>0)相切,则r= .
(t为参数),若斜率为1的直线经过抛物线C的焦点,且与圆(x-4)2+y2=r2(r>0)相切,则r= .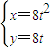 (t为参数),若斜率为1的直线经过抛物线C的焦点,且与圆(x-4)2+y2=r2(r>0)相切,则r= .
(t为参数),若斜率为1的直线经过抛物线C的焦点,且与圆(x-4)2+y2=r2(r>0)相切,则r= .