题目内容
已知实数x满足
求函数
|的最小值。
函数的最小值为2
解析:
原不等式等价于
于是，
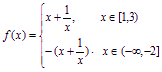当x∈[1，3）时，f（x）≥2（当且仅当x=1时取等号）；当 x∈（-∝，-2]时，可证得f（x）在（-∞，-2]上单调递减，故
（当且仅当x=-2时取等号）所以，所求函数的最小值为2。
练习册系列答案
相关题目
解析:
题目内容
已知实数x满足求函数|的最小值。
函数的最小值为2
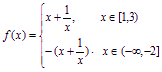原不等式等价于于是，当x∈[1，3）时，f（x）≥2（当且仅当x=1时取等号）；当 x∈（-∝，-2]时，可证得f（x）在（-∞，-2]上单调递减，故（当且仅当x=-2时取等号）所以，所求函数的最小值为2。
的值域．
的最大值和最小值。