题目内容
13．在同一个袋子中含有不同标号的红、黑两种颜色的小球共有8个，从红球中选取2粒，从黑球中选取1粒，共有30种不同的选法，其中黑球至多有（ ）| A． | 2粒 | B． | 4粒 | C． | 3粒 | D． | 5粒 |
分析 设红球有x粒，则黑球有8-x粒，从红球中选取2粒，从黑球中选取1粒，共有30种不同的选法，是组合问题，得到关于x的等式Cx2C8-x1=30，解出x即可．
解答 解：设红球有x粒，则黑球有8-x粒，
从红球中选取2粒，从黑球中选取1粒，共有30种不同的选法，是组合问题，
∴Cx2C8-x1=30，
∴x（x-1）（8-x）=30×2=2×6×5，或x（x-1）（8-x）=3×4×5．
∴x=6，8-6=2．或x=5，8-5=3．
黑球有：2或3粒．
故选：C．
点评 本题考查排列、组合的综合运用，注意排列与组合的区别，由x（x-1）（8-x）=60解出x的值运算量与难度都比较大，此时可以验证选项，进而选出答案．
练习册系列答案
相关题目
4．设向量$\overrightarrow{a}$=（cosα，$\frac{\sqrt{2}}{2}$）的模为$\frac{\sqrt{3}}{2}$，则cos2α=（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{\sqrt{3}}{2}$ | C． | -$\frac{1}{4}$ | D． | -$\frac{1}{2}$ |
8．
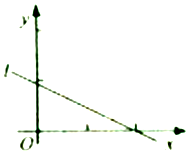设（x1，y1），（x2，y2），…，（xn，yn）是变量x和y的n个样本点，直线l是由这些样本点通过最小二乘法得到的线性回归直线（如图），以下结论中正确的是（ ）
设（x1，y1），（x2，y2），…，（xn，yn）是变量x和y的n个样本点，直线l是由这些样本点通过最小二乘法得到的线性回归直线（如图），以下结论中正确的是（ ）| A． | x和y的相关系数在-1和0之间 | |
| B． | x和y的相关系数为直线l的斜率 | |
| C． | 当n为偶数时，分布在l两侧的样本点的个数一定相同 | |
| D． | 所有样本点（xi，yi）（i=1，2，…，n）都在直线l上 |
18．已知X的分布列如表：
且b2=ac，$a=\frac{1}{2}$，则E（X）=（ ）
| X | -1 | 0 | 1 | 2 |
| P | a | b | c | $\frac{5}{18}$ |
| A． | $\frac{1}{9}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{2}$ | D． | $\frac{2}{3}$ |