题目内容
已知 ,
,  是椭圆的两个焦点,若满足
是椭圆的两个焦点,若满足 的点M总在椭圆的内部,则椭圆离心率的取值范围是( )
的点M总在椭圆的内部,则椭圆离心率的取值范围是( )
| A.(0, 1) | B. | C. | D. |
B
解析试题分析:设椭圆的半长轴、半短轴、半焦距分别为a,b,c,
因为 ,∴M点的轨迹是以原点O为圆心,半焦距c为半径的圆.
,∴M点的轨迹是以原点O为圆心,半焦距c为半径的圆.
又M点总在椭圆内部,
∴该圆内含于椭圆,即c<b,c2<b2=a2-c2.
∴e2= <
< ,∴0<e<
,∴0<e< ,故选C.
,故选C.
考点:本题主要考查椭圆的几何性质,圆的定义。
点评:典型题,本题突出考查椭圆的几何性质,圆的定义,有较浓的“几何味”。

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
q是第三象限角,方程x2+y2sinq=cosq表示的曲线是( )
| A.焦点在y轴上的双曲线 | B.焦点在y轴上的椭圆 |
| C.焦点在x轴上的双曲线 | D.焦点在x轴上的椭圆 |
如果方程 表示焦点在
表示焦点在 轴上的椭圆,则
轴上的椭圆,则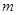 的取值范围是
的取值范围是
A. | B. | C. | D. |
设 ,则双曲线
,则双曲线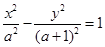 的离心率
的离心率 的取值范围是 ( )
的取值范围是 ( )
A. | B. | C. | D. |
已知椭圆 和双曲线
和双曲线 有公共的焦点,那么双曲线的渐近线方程是( )
有公共的焦点,那么双曲线的渐近线方程是( )
A. | B. | C.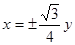 | D. |
已知抛物线 上的焦点
上的焦点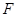 ,点
,点 在抛物线上,点
在抛物线上,点 ,则要使
,则要使 的值最小的点
的值最小的点 的坐标为
的坐标为
A. | B. | C.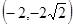 | D. |
若椭圆中心在原点,对称轴为坐标轴,长轴长为 ,离心率为
,离心率为 ,则该椭圆的方程为( )
,则该椭圆的方程为( )
A. | B. 或 或 |
C. | D. 或 或 |
 ,A为椭圆的左顶点,B、C在椭圆上,若四边形OABC为平行四边形,且
,A为椭圆的左顶点,B、C在椭圆上,若四边形OABC为平行四边形,且 ,则椭圆的离心率等于( )
,则椭圆的离心率等于( )
 B、
B、 C、
C、 D、
D、



