题目内容
对于n∈N*，用数学归纳法证明：1•n+2•（n-1）+3•（n-2）+…+（n-1）•2+n•1=
| 1 | 6 |
分析：根据数学归纳法证明的步骤，首先验证当n=1时成立，进而假设n=k时等式成立，证明n=k+1时，等式也成立；最后作答即可．
解答：证明：设f（n）=1•n+2•（n-1）+3•（n-2）+…+（n-1）•2+n•1．
（1）当n=1时，左边=1，右边=1，等式成立；
（2）设当n=k时等式成立，即1•k+2•（k-1）+3•（k-2）+…+（k-1）•2+k•1=
k（k+1）（k+2），
则当n=k+1时，
f（k+1）=1•（k+1）+2[（k+1）-1]+3[（k+1）-2]+…+[（k+1）-2]•3+[（k+1）-1]•2+（k+1）•1
=f（k）+1+2+3+…+k+（k+1）
=
k（k+1）（k+2）+
（k+1）（k+1+1）
=
（k+1）（k+2）（k+3）．
∴由（1）（2）可知当n∈N*时等式都成立．
（1）当n=1时，左边=1，右边=1，等式成立；
（2）设当n=k时等式成立，即1•k+2•（k-1）+3•（k-2）+…+（k-1）•2+k•1=
| 1 |
| 6 |
则当n=k+1时，
f（k+1）=1•（k+1）+2[（k+1）-1]+3[（k+1）-2]+…+[（k+1）-2]•3+[（k+1）-1]•2+（k+1）•1
=f（k）+1+2+3+…+k+（k+1）
=
| 1 |
| 6 |
| 1 |
| 2 |
=
| 1 |
| 6 |
∴由（1）（2）可知当n∈N*时等式都成立．
点评：本题考查数学归纳法的证明，需要牢记数学归纳法证明的步骤，特别要注意从k到k+1等式的形式的变化、区别．
练习册系列答案
相关题目
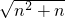＜n+1（n∈N*），某同学用数学归纳法的证明过程如下：
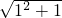＜1+1，不等式成立．
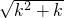＜k+1，则当n=k+1时，
=
＜
=
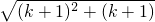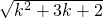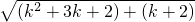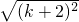=（k+1）+1，∴当n=k+1时，不等式成立．
,an+1=
(n∈N*).
(an-2)；
n（n+1）（n+2）．
＜n+1（n∈N*），某同学用数学归纳法的证明过程如下：
＜1+1，不等式成立．
＜k+1，则当n=k+1时，
=
＜
=
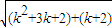=（k+1）+1，∴当n=k+1时，不等式成立．