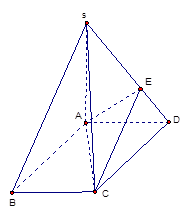
题目内容
如图,在直三棱柱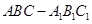 中,
中,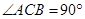 ,
,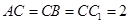 ,
,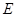 是
是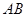 中点.
中点.

(1)求证: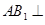 平面
平面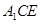 ;
;
(2)求直线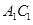 与平面
与平面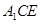 所成角的正弦值.
所成角的正弦值.
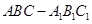 中,
中,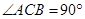 ,
,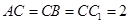 ,
,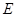 是
是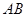 中点.
中点.
(1)求证:
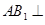 平面
平面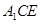 ;
;(2)求直线
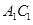 与平面
与平面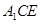 所成角的正弦值.
所成角的正弦值.(1)参考解析;(2)

试题分析:(1)直线与平面垂直的证明,对于理科生来说主要是以建立空间直角坐标系为主要方法,所以根据题意建立坐标系后,写出相应的点的坐标.根据向量证明向量
 与平面内的两个相交向量的数量积为零即可.
与平面内的两个相交向量的数量积为零即可.(2)证明直线与平面所成的角的正弦值,主要是通过求出平面的法向量与该直线的夹角的余弦值,再通过两角的互余关系转化为正弦值.
试题解析:(1)证明:因为
 是直三棱柱,
是直三棱柱,所以
 ,
,又
 ,
,即
 .
.如图所示,建立空间直角坐标系
 .
.
 ,
, ,
, ,
, ,
,所以
 ,
, ,
, .
.又因为
 ,
, ,
,所以
 ,
, ,
, 平面
平面 .
.(2)解:由(1)知,
 是平面
是平面 的法向量,
的法向量, ,
,则

 .
.设直线
 与平面
与平面 所成的角为
所成的角为 , 则
, 则
 .
.所以直线
 与平面
与平面 所成角的正弦值为
所成角的正弦值为 .
.
练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
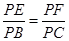 =λ.
=λ.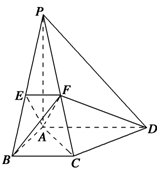
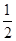 时,求异面直线BF与CD所成角的余弦值;
时,求异面直线BF与CD所成角的余弦值;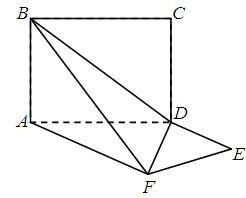
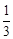 ,求AB的长.
,求AB的长. ABCD的底面是正方形,每条侧棱的长都是底面边长的
ABCD的底面是正方形,每条侧棱的长都是底面边长的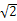 倍,P为侧棱SD上的点.
倍,P为侧棱SD上的点.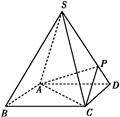
 为何值时,二面角A -A1D - C的平面角为600.
为何值时,二面角A -A1D - C的平面角为600.
 ,则
,则 ( )
( )



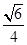
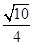
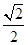
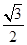
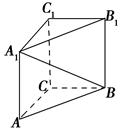
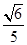
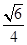
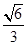
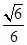
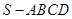 中,底面
中,底面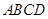 为平行四边形,
为平行四边形,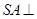 底面
底面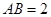 ,
,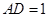 ,
,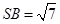 ,
,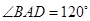 ,E在棱
,E在棱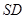 上, (Ⅰ) 当
上, (Ⅰ) 当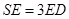 时,求证:
时,求证: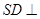 平面
平面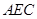 ; (Ⅱ) 当二面角
; (Ⅱ) 当二面角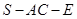 的大小为
的大小为 时,求直线
时,求直线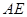 与平面
与平面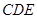 所成角的正弦值.
所成角的正弦值.