题目内容
已知函数 .
.
(1)若 ,求证:当
,求证:当 时,
时, ;
;
(2)若 在区间
在区间 上单调递增,试求
上单调递增,试求 的取值范围;
的取值范围;
(3)求证: .
.
 .
.(1)若
 ,求证:当
,求证:当 时,
时, ;
;(2)若
 在区间
在区间 上单调递增,试求
上单调递增,试求 的取值范围;
的取值范围;(3)求证:
 .
.(1) 详见解析;(2)  的取值范围
的取值范围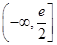 ;(3)详见解析.
;(3)详见解析.
 的取值范围
的取值范围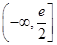 ;(3)详见解析.
;(3)详见解析.试题分析:(1) 当
 时,求证:当
时,求证:当 时,
时, ,将
,将 代入
代入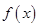 ,得
,得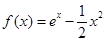 ,注意到
,注意到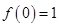 ,只要证明当
,只要证明当 时,
时,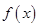 单调递增,则
单调递增,则 ,由于
,由于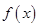 中含有指数函数,可对
中含有指数函数,可对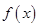 求导得
求导得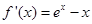 ,只需证明当
,只需证明当 时,
时,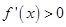 即可,注意到
即可,注意到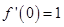 ,只要证明当
,只要证明当 时,
时,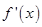 单调递增即可,因此令
单调递增即可,因此令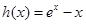 ,对
,对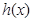 求导得
求导得 ,显然当
,显然当 时,
时, ,问题得证;(2) 求实数
,问题得证;(2) 求实数 的取值范围,由于
的取值范围,由于 在区间
在区间 上单调递增,则当
上单调递增,则当 时,
时,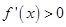 ,故对
,故对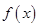 求导得
求导得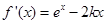 ,即当
,即当 时,
时,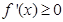 恒成立,即
恒成立,即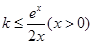 )恒成立,只需求出
)恒成立,只需求出 的最小值即可,令
的最小值即可,令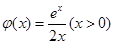 ,对
,对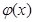 求导得
求导得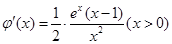 ,令导数等于零,解出
,令导数等于零,解出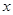 的值,从而的最小值,进而得实数
的值,从而的最小值,进而得实数 的取值范围;
的取值范围;(3)求证:
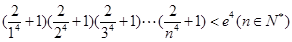 ,由(1) 知:当
,由(1) 知:当 时,
时,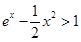 ,即
,即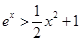 ,可得
,可得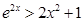 ,两边取对数得
,两边取对数得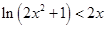 ,令
,令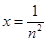 ,得
,得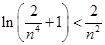 ,再令
,再令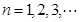 ,得
,得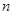 个式子相加,然后利用放缩法可证得结论.
个式子相加,然后利用放缩法可证得结论.试题解析:(1)
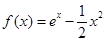 ,则h(x)=
,则h(x)=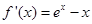 ,∴h′(x)=ex-1>0(x>0),
,∴h′(x)=ex-1>0(x>0),∴h(x)=f′(x)在(0,+∞)上递增,∴f′(x)>f′(0)=1>0,
∴f(x)=ex-
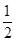 x2在(0,+∞)上单调递增,故f(x)>f(0)=1.( 4分)
x2在(0,+∞)上单调递增,故f(x)>f(0)=1.( 4分)(2) f′(x)=ex-2kx,下面求使
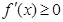 (x>0)恒成立的k的取值范围.
(x>0)恒成立的k的取值范围.若k≤0,显然f′(x)>0,f(x)在区间(0,+∞)上单调递增;
记φ(x)=ex-2kx,则φ′(x)=ex-2k,
当0<k<
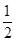 时,∵ex>e0=1, 2k<1,∴φ′ (x)>0,则φ(x)在(0,+∞)上单调递增,
时,∵ex>e0=1, 2k<1,∴φ′ (x)>0,则φ(x)在(0,+∞)上单调递增,于是f′(x)=φ(x)>φ(0)=1>0,∴f(x)在(0,+∞)上单调递增;
当k≥
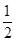 时,φ(x)=ex-2kx在(0,ln 2k)上单调递减,在(ln 2k,+∞)上单调递增,
时,φ(x)=ex-2kx在(0,ln 2k)上单调递减,在(ln 2k,+∞)上单调递增,于是f′(x)=φ(x)≥φ(ln 2k)=eln 2k-2kln 2k,
由eln 2k-2kln 2k≥0得2k-2kln 2k≥0,则
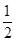 ≤k≤
≤k≤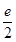 ,
,综上,k的取值范围为(-∞,
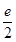 ]. 9分
]. 9分另解:(2)
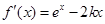 ,下面求使
,下面求使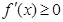 (x>0)恒成立的k的取值范围.
(x>0)恒成立的k的取值范围.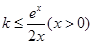 )恒成立。记
)恒成立。记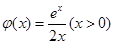
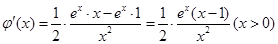
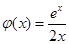 在
在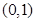 上单调递减,在
上单调递减,在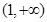 上单调递增。
上单调递增。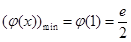
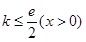
综上,k的取值范围为(-∞,
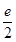 ].( 9分)
].( 9分)(3)由(1)知,对于x∈(0,+∞),有f(x)=ex>
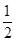 x2+1,∴e2x>2x2+1,
x2+1,∴e2x>2x2+1,则ln(2x2+1)<2x,从而有ln(
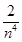 +1)<
+1)<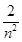 (n∈N*),
(n∈N*),于是ln(
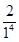 +1)+ln(
+1)+ln(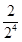 +1)+ln(
+1)+ln(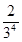 +1)+ +ln(
+1)+ +ln(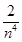 +1)<
+1)<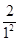 +
+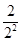 + +
+ +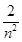 <
<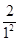 +
+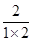 + +
+ +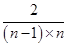 =2+2(1-
=2+2(1-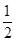 + +
+ +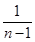 -
-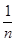 )=4-
)=4-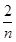 <4,故(
<4,故(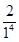 +1)(
+1)(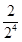 +1)(
+1)(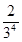 +1) (
+1) (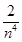 +1)<e4.( 14分)
+1)<e4.( 14分)另解:(3)由(1)知,对于x∈(0,+∞),有f(x)=ex>
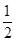 x2+1,∴e2x>2x2+1,
x2+1,∴e2x>2x2+1,则ln(2x2+1)<2x,从而有ln(
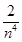 +1)<
+1)<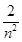 (n∈N*),
(n∈N*),又
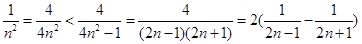
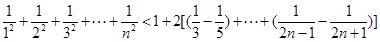
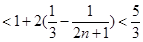
于是ln(
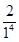 +1)+ln (
+1)+ln (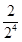 +1)+ln(
+1)+ln(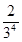 +1)+ +ln(
+1)+ +ln(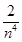 +1)<
+1)<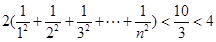
故(
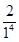 +1)(
+1)(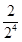 +1)(
+1)(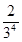 +1) (
+1) (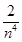 +1)<e4. ( 14分)
+1)<e4. ( 14分)
练习册系列答案
相关题目
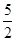 x+b在区间[0,2]上恰有两个不同的实数根,求实数b的取值范围;
x+b在区间[0,2]上恰有两个不同的实数根,求实数b的取值范围;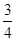 +
+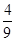 +…+
+…+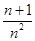 >ln(n+1)都成立.
>ln(n+1)都成立. ,
, .
. ,求函数
,求函数 的单调区间;
的单调区间; 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; ,若对任意的两个实数
,若对任意的两个实数 满足
满足 ,总存在
,总存在 ,使得
,使得
 成立,证明:
成立,证明: .
.
 的最小值;
的最小值; ,
, .
. 时,
时, 的图象与
的图象与 的图象有唯一的公共点;
的图象有唯一的公共点; 时,
时, 的取值范围.
的取值范围.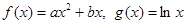 .
.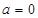 时,①若
时,①若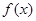 的图象与
的图象与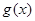 的图象相切于点
的图象相切于点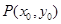 ,求
,求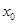 及
及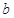 的值;
的值;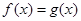 在
在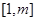 上有解,求
上有解,求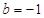 时,若
时,若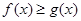 在
在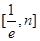 上恒成立,求
上恒成立,求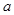 的取值范围.
的取值范围.
 时,求
时,求 的单调区间;
的单调区间; 时,
时, 恒成立,求
恒成立,求 的取值范围.
的取值范围. ;
;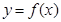 在
在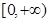 上单调递增;
上单调递增;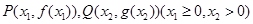 ,若直线PQ∥x轴,求P,Q两点间的最短距离.
,若直线PQ∥x轴,求P,Q两点间的最短距离.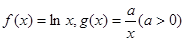 ,设
,设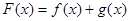
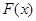 的单调区间
的单调区间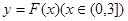 图象上任意一点
图象上任意一点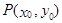 为切点的切线的斜率
为切点的切线的斜率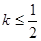 恒成立,求实数
恒成立,求实数 的最小值
的最小值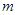 ,使得函数
,使得函数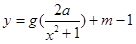 的图象与函数
的图象与函数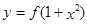 的图象恰有四个不同交点?若存在,求出实数
的图象恰有四个不同交点?若存在,求出实数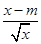 有解,求实数m的取值范围.
有解,求实数m的取值范围.