题目内容
如图,某园林单位准备绿化一块直径为BC的半圆形空地,△ABC的外面种草,△ABC的内接正方形PQRS为一水池,其余的地方种花,若BC=a,∠ABC=θ,设△ABC的面积为S1,正方形的面积为S2.
(1)用a,θ表示S1和S2;
(2)当a固定,θ变化时,求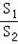 取最小值时的角.
取最小值时的角.
(1)用a,θ表示S1和S2;
(2)当a固定,θ变化时,求
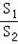 取最小值时的角.
取最小值时的角.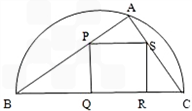
解:(1)在Rt△ABC中,AB=acosθ,AC=asinθ,
设正方形的边长为x则 ,
,
由BP+AP=AB,得 ,
,
故
所以
(2) ,
,
令t=sin2θ,因为 ,所以0<2θ<π,则t=sin2θ∈(0,1]
,所以0<2θ<π,则t=sin2θ∈(0,1]
所以 ,
,
 ,所以函数g(t)在(0,1]上递减,
,所以函数g(t)在(0,1]上递减,
因此当t=1时g(t)有最小值 ,
,
此时
所以当 时,“规划合理度”最小,最小值为
时,“规划合理度”最小,最小值为  .
.

设正方形的边长为x则
 ,
,由BP+AP=AB,得
 ,
,故

所以

(2)
 ,
,令t=sin2θ,因为
 ,所以0<2θ<π,则t=sin2θ∈(0,1]
,所以0<2θ<π,则t=sin2θ∈(0,1]所以
 ,
, ,所以函数g(t)在(0,1]上递减,
,所以函数g(t)在(0,1]上递减,因此当t=1时g(t)有最小值
 ,
,此时

所以当
 时,“规划合理度”最小,最小值为
时,“规划合理度”最小,最小值为  .
.
练习册系列答案
相关题目
 如图,某园林单位准备绿化一块直径为BC的半圆形空地,△ABC的外面种草,△ABC的内接正方形PQRS为一水池,其余的地方种花,若BC=a,∠ABC=θ,设△ABC的面积为S1,正方形的面积为S2.
如图,某园林单位准备绿化一块直径为BC的半圆形空地,△ABC的外面种草,△ABC的内接正方形PQRS为一水池,其余的地方种花,若BC=a,∠ABC=θ,设△ABC的面积为S1,正方形的面积为S2.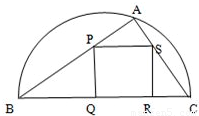 如图,某园林单位准备绿化一块直径为BC的半圆形空地,△ABC的外面种草,△ABC的内接正方形PQRS为一水池,其余的地方种花,若BC=a,∠ABC=θ,设△ABC的面积为S1,正方形的面积为S2.
如图,某园林单位准备绿化一块直径为BC的半圆形空地,△ABC的外面种草,△ABC的内接正方形PQRS为一水池,其余的地方种花,若BC=a,∠ABC=θ,设△ABC的面积为S1,正方形的面积为S2. 取最小值时的角.
取最小值时的角.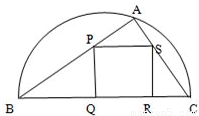 如图,某园林单位准备绿化一块直径为BC的半圆形空地,△ABC的外面种草,△ABC的内接正方形PQRS为一水池,其余的地方种花,若BC=a,∠ABC=θ,设△ABC的面积为S1,正方形的面积为S2.
如图,某园林单位准备绿化一块直径为BC的半圆形空地,△ABC的外面种草,△ABC的内接正方形PQRS为一水池,其余的地方种花,若BC=a,∠ABC=θ,设△ABC的面积为S1,正方形的面积为S2.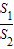 取最小值时的角.
取最小值时的角.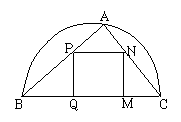 (满分14分)如图,某园林单位准备绿化一块直径为BC的半圆形空间,△ABC外的地方种草,△ABC的内接正方形MNPQ为水池,其余地方种花。若BC=a,∠ABC=
(满分14分)如图,某园林单位准备绿化一块直径为BC的半圆形空间,△ABC外的地方种草,△ABC的内接正方形MNPQ为水池,其余地方种花。若BC=a,∠ABC= ,设△ABC面积为S1,正方形MNPQ的面积为S2.
,设△ABC面积为S1,正方形MNPQ的面积为S2.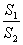 最小值及此时
最小值及此时