题目内容
若{| i |
| j |
| a |
| i |
| j |
| a |
分析:通过配方和利用二次函数的单调性可得x2+x+1,-x2+x-1的取值范围,进而判断出答案.
解答:解:∵x2+x+1=(x+
)2+
≥
,-(x2-x+1)=-(x-
)2-
≤-
,
∴
对应的点(x2+x+1,-x2+x-1)位于第四象限.
故答案为:四.
| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 4 |
| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 4 |
∴
| a |
故答案为:四.
点评:本题考查了配方法、二次函数的单调性、向量的几何意义,属于基础题.

练习册系列答案
相关题目
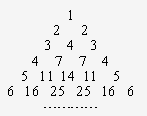 我们用部分自然数构造如下的数表:用aij(i≥j)表示第i行第j个数(i、j为正整数),使ai1=aii=i;每行中的其余各数分别等于其“肩膀”上的两个数之和(第一、二行除外,如图),设第n(n为正整数)行中各数之和为bn.
我们用部分自然数构造如下的数表:用aij(i≥j)表示第i行第j个数(i、j为正整数),使ai1=aii=i;每行中的其余各数分别等于其“肩膀”上的两个数之和(第一、二行除外,如图),设第n(n为正整数)行中各数之和为bn.