题目内容
已知函数 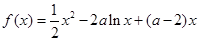 ,
,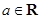 .
.
(1)当 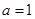 时,求函数
时,求函数 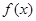 的最小值;
的最小值;
(2)当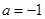 时,求证:无论
时,求证:无论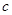 取何值,直线
取何值,直线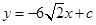 均不可能与函数
均不可能与函数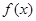 相切;
相切;
(3)是否存在实数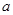 ,对任意的
,对任意的 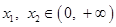 ,且
,且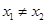 ,有
,有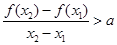 恒成立,若存在求出
恒成立,若存在求出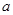 的取值范围,若不存在,说明理由。
的取值范围,若不存在,说明理由。
(1)-2ln2;(2)详见解析;(3)存在实数,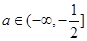 .
.
解析试题分析:(1)把a=1代入函数解析式,求导后得到导函数的零点,由导函数的零点对定义域分段,根据导函数在各区间段内的符号得到原函数的单调性,从而求出函数f(x)的最小值;(2)把a=-1代入原函数,求出导函数后利用基本不等式求出导函数的值域,从而说明无论c 取何值,直线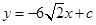 均不可能与函数f(x)相切;(3)假设存在实数a使得对任意的
均不可能与函数f(x)相切;(3)假设存在实数a使得对任意的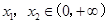 ,且
,且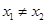 ,有
,有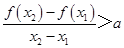 恒成立,假设
恒成立,假设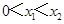 ,则
,则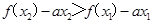 恒成立,构造辅助函数
恒成立,构造辅助函数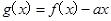 ,只要使函数g(x)在定义域内为增函数即可,利用其导函数恒大于等于0可求解a的取值范围.
,只要使函数g(x)在定义域内为增函数即可,利用其导函数恒大于等于0可求解a的取值范围.
解;(1)显然函数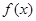 的定义域为
的定义域为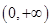 ,
,
当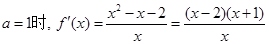 .
.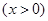
∴ 当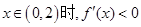 ,
,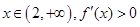 .
.
∴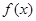 在
在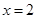 时取得最小值,其最小值为
时取得最小值,其最小值为 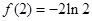 .
.
(2)∵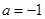
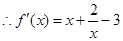 ,
,
假设直线与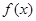 相切,设切点为
相切,设切点为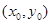 ,则
,则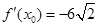
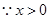
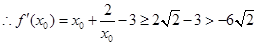 所以
所以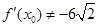 所以无论
所以无论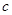 取何值,直线
取何值,直线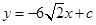 均不可能与函数
均不可能与函数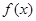 相切。
相切。
(3)假设存在实数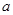 使得对任意的
使得对任意的 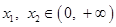 ,且
,且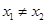 ,有
,有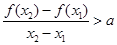 ,恒成立,不妨设
,恒成立,不妨设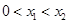 ,只要
,只要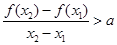 ,即:
,即: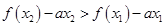
令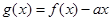 ,只要
,只要 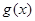 在
在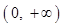 为增函数
为增函数
又函数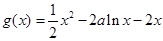 .
.
考查函数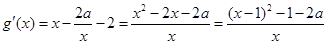
要使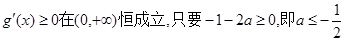 ,
,
故存在实数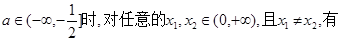
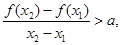 恒成立.
恒成立.
考点:1.利用导数求闭区间上函数的最值;2.利用导数研究曲线上某点切线方程.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
 (
( )
) 时,求函数
时,求函数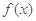 的极值;(2)当
的极值;(2)当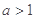 时,讨论
时,讨论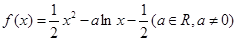 .
.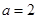 时,求曲线
时,求曲线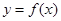 在点
在点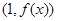 处的切线方程;
处的切线方程;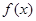 的单调区间;
的单调区间; 都有
都有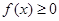 恒成立,求实数
恒成立,求实数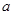 的取值范围.
的取值范围.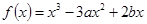 在x=1处有极小值-1,
在x=1处有极小值-1,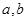 的值; (2)求出
的值; (2)求出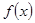 的单调区间.
的单调区间. (f′(x)是f(x)的导数)在区间(t,3)上总不是单调函数,求m的取值范围;
(f′(x)是f(x)的导数)在区间(t,3)上总不是单调函数,求m的取值范围; ×…×
×…×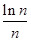 <
< (n≥2,n∈N*).
(n≥2,n∈N*).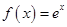 .
.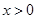 时,设
时,设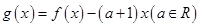 .讨论函数
.讨论函数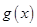 的单调性;
的单调性;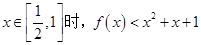 .
.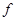 (
( ) =
) =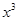 ,g (
,g (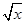 。
。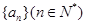 满足
满足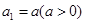 ,
,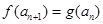 ,证明:存在常数M,使得对于任意的
,证明:存在常数M,使得对于任意的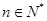 ,都有
,都有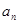 ≤
≤ 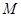 .
.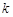
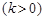 .现已知相距18
.现已知相距18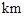 的A,B两家化工厂(污染源)的污染强度分别为
的A,B两家化工厂(污染源)的污染强度分别为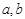 ,它们连线上任意一点C处的污染指数
,它们连线上任意一点C处的污染指数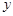 等于两化工厂对该处的污染指数之和.设
等于两化工厂对该处的污染指数之和.设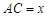 (
(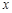 的函数; (2)若
的函数; (2)若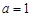 ,且
,且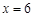 时,
时,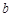 的值.
的值.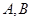 所在直线的距离)的抛物线形的一部分,现要将其缺口边界裁剪为等腰梯形.
所在直线的距离)的抛物线形的一部分,现要将其缺口边界裁剪为等腰梯形.