题目内容
已知F1、F2是椭圆 的焦点,P是椭圆上一点,且∠F1PF2=90°,则椭圆的离心率e的取值范围是 .
的焦点,P是椭圆上一点,且∠F1PF2=90°,则椭圆的离心率e的取值范围是 .
【答案】分析:由条件知,以F1F2为直径的圆与椭圆有交点,故有圆的半径大于或等于短半轴的长度.
解答:解:∵F1、F2是椭圆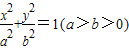 的焦点,
的焦点,
P是椭圆上一点,且∠F1PF2=90°,
∴以F1F2为直径的圆与椭圆有交点,圆的半径r=c≥b,
∴e2=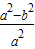 ≥
≥ ,2e2≥1,
,2e2≥1,
∴e≥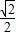 ,又0<e<1,
,又0<e<1,
∴椭圆的离心率e的取值范围是[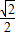 ,1),
,1),
故答案为[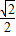 ,1).
,1).
点评:本题考查椭圆的标准方程和简单性质的应用.
解答:解:∵F1、F2是椭圆
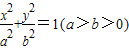 的焦点,
的焦点,P是椭圆上一点,且∠F1PF2=90°,
∴以F1F2为直径的圆与椭圆有交点,圆的半径r=c≥b,
∴e2=
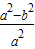 ≥
≥ ,2e2≥1,
,2e2≥1,∴e≥
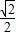 ,又0<e<1,
,又0<e<1,∴椭圆的离心率e的取值范围是[
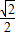 ,1),
,1),故答案为[
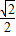 ,1).
,1).点评:本题考查椭圆的标准方程和简单性质的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目