题目内容
已知等差数列{an}满足a2≤2，a3≤4，a1+a4≥4，当a4取得最大值时，数列{an}的公差为 ．
考点：等差数列的性质
专题：等差数列与等比数列
分析：设数列{an}的公差为d，根据题意和等差数列的通项公式列出不等式组，设a1=x，d=y转化线性规划问题，画出可行域和初始直线，再求出a4最大值和对应的公差的值．
解答：
解：设数列{an}的公差为d，
因为a2≤2，a3≤4，a1+a4≥4，所以
，①
设a1=x，d=y，则①变为：
，且a4=a1+3d=x+3y
画出可行域如右图阴影部分所示：
当直线y=-
x+
a4经过点A时截距最大，即a4最大，
由
得，
x=-4，y=4，
此时a4=-4+12=8，
此时a1=-4，d=4，
所以数列{an}的公差为4，
故答案为：4．
因为a2≤2，a3≤4，a1+a4≥4，所以
|
设a1=x，d=y，则①变为：
|
画出可行域如右图阴影部分所示：
当直线y=-
| 1 |
| 3 |
| 1 |
| 3 |
由
|
x=-4，y=4，
此时a4=-4+12=8，
此时a1=-4，d=4，
所以数列{an}的公差为4，
故答案为：4．
点评：本题考查等差数列的通项公式，换元法的灵活应用，以及线性规划问题，考查转化能力，属于难题．
练习册系列答案
相关题目
设{an}是公差不为零的等差数列，a2=2，且a1，a3，a9成等比数列，则数列{an}的前n项和Sn=（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
命题p：?x＞0，ex＞1，则?p是（ ）
| A、?x0≤0，ex0≤1 |
| B、?x0＞0，ex0≤1 |
| C、?x＞0，ex≤1 |
| D、?x≤0，ex≤1 |
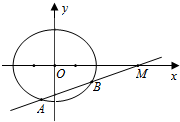如图所示，椭圆C：