题目内容
3.-885°化成2kπ+α(0≤α≤2π,k∈Z)的形式是-6π+$\frac{13π}{12}$.分析 利用360°=2π,把-885°转化为-6π+α的形式即可.
解答 解:-885°=-1080°+195°=-6π+$\frac{13π}{12}$.
故答案为:-6π+$\frac{13π}{12}$.
点评 本题是基础题,考查角度与弧度的转化,注意题目0≤α≤2π的条件的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.若抛物线的顶点在原点,焦点是双曲线$\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{4}$=1的顶点,则抛物线的方程是( )
| A. | y2=4x,y2=-4x | B. | y2=6x,y2=-6x | C. | y2=10x,y2=-10x | D. | y2=12x,y2=-12x |
8.在等差数列{an}中,若a1+a2+a3=32,a11+a12+a13=118,则a4+a10=( )
| A. | 45 | B. | 50 | C. | 75 | D. | 60 |
12.函数f(x)=x2+px+q对任意的x均有f(1+x)=f(1-x),那么f(0)、f(-1)、f(1)的大小关系是( )
| A. | f(1)<f(-1)<f(0) | B. | f(1)<f(0)<f(-1) | C. | f(0)<f(-1)<f(1) | D. | f(-1)<f(0)<f(1) |
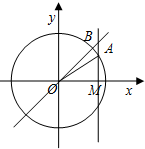 如图,角α的始边与x轴的非负半轴重合,终边与单位圆交于点A,直线MA垂直x轴于点M,B是直线y=x与MA的交点,设f(α)=$\overrightarrow{OA}•\overrightarrow{OB}$.
如图,角α的始边与x轴的非负半轴重合,终边与单位圆交于点A,直线MA垂直x轴于点M,B是直线y=x与MA的交点,设f(α)=$\overrightarrow{OA}•\overrightarrow{OB}$.