题目内容
【题目】已知函数f(x)= ![]() .
.
(1)求函数f(x)的单调区间;
(2)若g(x)=xf(x)+mx在区间(0,e]上的最大值为﹣3,求m的值;
(3)若x≥1时,有不等式f(x)≥ ![]() 恒成立,求实数k的取值范围.
恒成立,求实数k的取值范围.
【答案】
(1)解:易知f(x)定义域为(0,+∞), ![]() ,令f'(x)=0,得x=1.
,令f'(x)=0,得x=1.
当0<x<1时,f'(x)>0;当x>1时,f'(x)<0.
∴f(x)在(0,1)上是增函数,在(1,+∞)上是减函数
(2)解:∵g(x)=1+lnx+mx, ![]() ,x∈(0,e],
,x∈(0,e],
①若m≥0,则g'(x)≥0,从而g(x)在(0,e]上是增函数,∴g(x)max=g(e)=me+2≥0,不合题意.
②若m<0,则由g'(x)>0,即 ![]() ,若
,若 ![]() ,g(x)在(0,e]上是增函数,
,g(x)在(0,e]上是增函数,
由①知不合题意.
由g'(x)<0,即 ![]() .
.
从而g(x)在 ![]() 上是增函数,在
上是增函数,在 ![]() 为减函数,
为减函数,
∴ ![]() ,令ln(
,令ln( ![]() )=﹣3,所以m=﹣e3,
)=﹣3,所以m=﹣e3,
∵ ![]() ,∴所求的m=﹣e3
,∴所求的m=﹣e3
(3)解:∵x≥1时, ![]() 恒成立,∴k≤(x+1)f(x)=lnx+
恒成立,∴k≤(x+1)f(x)=lnx+ ![]() +
+ ![]() +1,
+1,
令 ![]() ,
,
∴ ![]() 恒大于0,
恒大于0,
∴h(x)在[1,+∞)为增函数,
∴h(x)min=h(1)=2,∴k≤2
【解析】(1)求出函数的定义域,函数的导数,求出极值点,判断导函数符号,然后求解单调区间.(2)求出 ![]() ,x∈(0,e],通过①若m≥0,②若m<0,判断函数的单调性,求解函数的最值,然后求m.(3)利用x≥1时,
,x∈(0,e],通过①若m≥0,②若m<0,判断函数的单调性,求解函数的最值,然后求m.(3)利用x≥1时, ![]() 恒成立,分离变量,构造函数
恒成立,分离变量,构造函数 ![]() ,利用函数的导数,求解函数的最值,推出结果即可.
,利用函数的导数,求解函数的最值,推出结果即可.

【题目】下表是某厂的产量x与成本y的一组数据:
产量x(千件) | 2 | 3 | 5 | 6 |
成本y(万元) | 7 | 8 | 9 | 12 |
(Ⅰ)根据表中数据,求出回归直线的方程 ![]() =
= ![]() x
x ![]() (其中
(其中 ![]() =
= 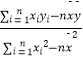 ,
, ![]() =
= ![]() ﹣
﹣ ![]() )
)
(Ⅱ)预计产量为8千件时的成本.