Question

如图，在正四棱柱ABCD-A₁B₁C₁D₁中，已知AB=2，AA₁=5，
E、F分别为D₁D、B₁B上的点，且DE=B₁F=1．
（Ⅰ）求证：BE⊥平面ACF；
（Ⅱ）求点E到平面ACF的距离．

Answer 1

分析：（I）以D为原点，DA、DC、DD₁所在直线分别为x、y、z轴建立空间直角坐标系，写出要用的点的坐标，要证明线与面垂直，只要证明这条直线与平面上的两条直线垂直．
（II）

BE

为平面ACF的一个法向量，向量

AE

在

BE

上的射影长即为E到平面ACF的距离，根据点到面的距离公式得到结果．

解答：解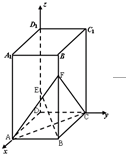：（Ⅰ）如图，以D为原点，DA、DC、DD₁所在直线分别为x、y、z轴
建立空间直角坐标系，则D（0，0，0），A（2，0，0），B（2，2，0），
C（0，2，0），D₁（0，0，5），E（0，0，1），F（2，2，4）
∴

AC

=（-2，2，0），

AF

=（0，2，4），

BE

=（-2，-2，1），

AE

=（-2，0，1）．   
∴

BE

•

AC

=0  

BE

•

AF

=0
∴BE⊥AC，BE⊥AF，且AC∩AF=A
∴BE⊥平面ACF
（Ⅱ）由（Ⅰ）知，

BE

为平面ACF的一个法向量    
∴向量

AE

在

BE

上的射影长即为E到平面ACF的距离，设为d
于是 d=

AE • BE

| BE |

=

5

3

故点E到平面ACF的距离

5

3

点评：本题是一个立体几何的综合题目，题目的第一问，用空间向量来证明，实际上若不是为了后一问应用方便，可以采用几何法来证明．