题目内容
在数列{an}中,已知a1=2,an+1=| 2an |
| an+1 |
(Ⅰ)证明数列{
| 1 |
| an |
(Ⅱ)求证:
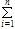 ai(ai-1)<3
ai(ai-1)<3
分析:(1)对an+1=
两边求倒数得
-1=
(
-1),由a1=2得出数列{
-1}是首项为-
,公比为
的等比数列.写出其通项公式化简可得数列{an}的通项公式;
(2)利用ai(ai-1)=
<
=
=
-
证出即可.
| 2an |
| an+1 |
| 1 |
| an+1 |
| 1 |
| 2 |
| 1 |
| an |
| 1 |
| an |
| 1 |
| 2 |
| 1 |
| 2 |
(2)利用ai(ai-1)=
| 2i |
| (2i-1)2 |
| 2i |
| (2i-1)(2i-2) |
| 2i-1 |
| (2i-1)(2i-1-1) |
| 1 |
| 2i-1-1 |
| 1 |
| 2i-1 |
解答:(Ⅰ)解:由a1=2,an+1=
得,对n∈N*,an≠0.
从而由an+1=
两边取倒数得,
=
+
.
即
-1=
(
-1),
∵a1=2,
-1=-
.
∴数列{
-1}是首项为-
,公比为
的等比数列.
∴
-1=-
•
n-1=-(-
)n
∴
=1-
=
.∴an=
.
故数列{an}的通项公式是an=
.
(Ⅱ)∵an=
,
∴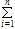 ai(ai-1)=
ai(ai-1)=
(i=1,2,,n),
当i≥2时,
∵ai(ai-1)=
<
=
=
-
,
∴ai(ai-1)=a1(a1-1)+a2(a2-1)+…+an(an-1)
=
+
+…+
<
+(
-
)+(
-
)+…+(
-
)
=2+1-
=3-
<3.
| 2an |
| an+1 |
从而由an+1=
| 2an |
| an+1 |
| 1 |
| an+1 |
| 1 |
| 2 |
| 1 |
| 2an |
即
| 1 |
| an+1 |
| 1 |
| 2 |
| 1 |
| an |
∵a1=2,
| 1 |
| a1 |
| 1 |
| 2 |
∴数列{
| 1 |
| an |
| 1 |
| 2 |
| 1 |
| 2 |
∴
| 1 |
| an |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴
| 1 |
| an |
| 1 |
| 2n |
| 2n-1 |
| 2n |
| 2n |
| 2n-1 |
故数列{an}的通项公式是an=
| 2n |
| 2n-1 |
(Ⅱ)∵an=
| 2n |
| 2n-1 |
∴
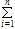 ai(ai-1)=
ai(ai-1)=| 2i |
| (2i-1)2 |
当i≥2时,
∵ai(ai-1)=
| 2i |
| (2i-1)2 |
| 2i |
| (2i-1)(2i-2) |
| 2i-1 |
| (2i-1)(2i-1-1) |
| 1 |
| 2i-1-1 |
| 1 |
| 2i-1 |
∴ai(ai-1)=a1(a1-1)+a2(a2-1)+…+an(an-1)
=
| 21 |
| (21-1)2 |
| 22 |
| (22-1)2 |
| 2n |
| (2n-1)2 |
<
| 21 |
| (21-1)2 |
| 1 |
| 21-1 |
| 1 |
| 22-1 |
| 1 |
| 22-1 |
| 1 |
| 23-1 |
| 1 |
| 2n-1-1 |
| 1 |
| 2n-1 |
=2+1-
| 1 |
| 2n-1 |
=3-
| 1 |
| 2n-1 |
点评:考查学生对等比关系的判断能力,会利用数列的递推式的能力,以及不等式的证明能力.

练习册系列答案
相关题目