题目内容
已知双曲线 -
- =1(a>0,b>0).它的两条渐近线截直线x=-
=1(a>0,b>0).它的两条渐近线截直线x=- •所得线段的长度恰好为它的一个焦点到一条渐近线的距离,则该双曲线的离心率为
•所得线段的长度恰好为它的一个焦点到一条渐近线的距离,则该双曲线的离心率为
- A.

- B.

- C.2
- D.3
C
分析:求出两条渐近线截直线x=- •所得线段的长度,再求出双曲线的一个焦点到渐近线 的距离,利用等量关系建立方程,求出离心率
•所得线段的长度,再求出双曲线的一个焦点到渐近线 的距离,利用等量关系建立方程,求出离心率 的值.
的值.
解答:由题意得,渐近线方程为y=± x,bx±ay=0,由
x,bx±ay=0,由 得,
得,
渐近线截直线x=- 所得线段的一个交点为(-
所得线段的一个交点为(- ,-
,- ),
),
同理求得另一个交点为(- ,
, ),
),
∴它的两条渐近线截直线x=- ,所得线段的长度为
,所得线段的长度为 .
.
双曲线的一个焦点(c,0)到渐近线 bx-ay=0的距离 d= =
= =b,
=b,
∴ =b,
=b, =2,
=2,
故选C.
点评:本题考查双曲线的标准方程,点到直线的距离公式以及双曲线的简单性质的应用,求出两条渐近线截直线x=- •所得线段的长度是解题的突破口.
•所得线段的长度是解题的突破口.
分析:求出两条渐近线截直线x=-
 •所得线段的长度,再求出双曲线的一个焦点到渐近线 的距离,利用等量关系建立方程,求出离心率
•所得线段的长度,再求出双曲线的一个焦点到渐近线 的距离,利用等量关系建立方程,求出离心率 的值.
的值.解答:由题意得,渐近线方程为y=±
 x,bx±ay=0,由
x,bx±ay=0,由 得,
得,渐近线截直线x=-
 所得线段的一个交点为(-
所得线段的一个交点为(- ,-
,- ),
),同理求得另一个交点为(-
 ,
, ),
),∴它的两条渐近线截直线x=-
 ,所得线段的长度为
,所得线段的长度为 .
.双曲线的一个焦点(c,0)到渐近线 bx-ay=0的距离 d=
 =
= =b,
=b,∴
 =b,
=b, =2,
=2,故选C.
点评:本题考查双曲线的标准方程,点到直线的距离公式以及双曲线的简单性质的应用,求出两条渐近线截直线x=-
 •所得线段的长度是解题的突破口.
•所得线段的长度是解题的突破口. 
练习册系列答案
相关题目
 =1(a>0,b>0)的离心率为
=1(a>0,b>0)的离心率为 ,右准线方程为
,右准线方程为 .
. =1(a>0,b>0)的离心率为
=1(a>0,b>0)的离心率为 ,右准线方程为
,右准线方程为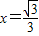 .
. =1(a>0,b>0)的离心率为
=1(a>0,b>0)的离心率为 ,右准线方程为
,右准线方程为 .
. =1(a>0,b>0)的离心率为
=1(a>0,b>0)的离心率为 ,右准线方程为
,右准线方程为 .
.