题目内容
已知椭圆的右顶点为A,离心率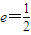 ,过左焦点F(-1,0)作直线l与椭圆交于点P,Q,直线AP,AQ分别与直线x=-4交于点M,N.
,过左焦点F(-1,0)作直线l与椭圆交于点P,Q,直线AP,AQ分别与直线x=-4交于点M,N.(Ⅰ)求椭圆的方程;
(Ⅱ)证明以线段MN为直径的圆经过焦点F.
【答案】分析:(Ⅰ)由离心率 ,过左焦点F(-1,0),可求得 c=1,a=2,从而可求b=
,过左焦点F(-1,0),可求得 c=1,a=2,从而可求b=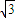 ,进而可得椭圆方程;
,进而可得椭圆方程;
(Ⅱ) 斜率存在时,设直线l方程为 y=k(x+1),与椭圆方程联立,消去y 整理得(3+4k2)x2+8k2x+4k2-12=0.进而可求M,N的坐标,从而可证 ;斜率不存在时,同理可证
;斜率不存在时,同理可证 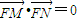 ,从而以线段MN为直径的圆经过定点F
,从而以线段MN为直径的圆经过定点F
解答:解:(Ⅰ)由已知 c=1,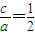 ,
,
∴a=2,b=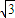 ,
,
∴椭圆方程为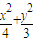 =1.--------------(5分)
=1.--------------(5分)
证明:(Ⅱ) 设直线l方程为 y=k(x+1),
由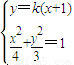 得(3+4k2)x2+8k2x+4k2-12=0.
得(3+4k2)x2+8k2x+4k2-12=0.
设P(x1,y1),Q(x2,y2),则x1+x2=-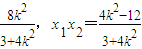 .-----(7分)
.-----(7分)
设M(-4,yM),N(-4,yN),则由A,P,M共线,得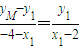 ,有 yM=-
,有 yM=-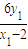 .同理 yN=-
.同理 yN=-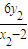 .
.
∴yMyN=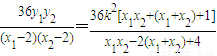 .------(9分)
.------(9分)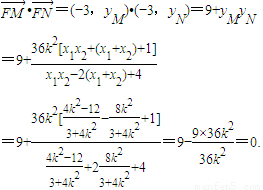
∴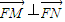 ,即FM⊥FN,以线段MN为直径的圆经过点F;----(12分)
,即FM⊥FN,以线段MN为直径的圆经过点F;----(12分)
当直线l的斜率不存在时,不妨设M(-4,3),N(-4,-3).则有 )=9-9=0,
)=9-9=0,
∴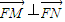 ,即FM⊥FN,以线段MN为直径的圆经过点F.
,即FM⊥FN,以线段MN为直径的圆经过点F.
综上所述,以线段MN为直径的圆经过定点F.-----------(14分)
点评:本题以椭圆的几何性质为载体,考查椭圆的标准方程,考查直线与椭圆的位置关系,同时考查向量与解析几何的交汇,综合性强.
 ,过左焦点F(-1,0),可求得 c=1,a=2,从而可求b=
,过左焦点F(-1,0),可求得 c=1,a=2,从而可求b=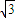 ,进而可得椭圆方程;
,进而可得椭圆方程;(Ⅱ) 斜率存在时,设直线l方程为 y=k(x+1),与椭圆方程联立,消去y 整理得(3+4k2)x2+8k2x+4k2-12=0.进而可求M,N的坐标,从而可证
 ;斜率不存在时,同理可证
;斜率不存在时,同理可证 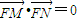 ,从而以线段MN为直径的圆经过定点F
,从而以线段MN为直径的圆经过定点F解答:解:(Ⅰ)由已知 c=1,
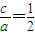 ,
,∴a=2,b=
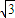 ,
,∴椭圆方程为
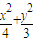 =1.--------------(5分)
=1.--------------(5分)证明:(Ⅱ) 设直线l方程为 y=k(x+1),
由
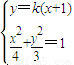 得(3+4k2)x2+8k2x+4k2-12=0.
得(3+4k2)x2+8k2x+4k2-12=0.设P(x1,y1),Q(x2,y2),则x1+x2=-
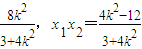 .-----(7分)
.-----(7分)设M(-4,yM),N(-4,yN),则由A,P,M共线,得
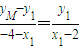 ,有 yM=-
,有 yM=-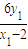 .同理 yN=-
.同理 yN=-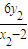 .
.∴yMyN=
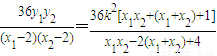 .------(9分)
.------(9分)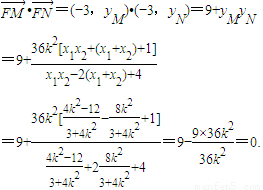
∴
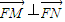 ,即FM⊥FN,以线段MN为直径的圆经过点F;----(12分)
,即FM⊥FN,以线段MN为直径的圆经过点F;----(12分)当直线l的斜率不存在时,不妨设M(-4,3),N(-4,-3).则有
 )=9-9=0,
)=9-9=0,∴
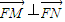 ,即FM⊥FN,以线段MN为直径的圆经过点F.
,即FM⊥FN,以线段MN为直径的圆经过点F.综上所述,以线段MN为直径的圆经过定点F.-----------(14分)
点评:本题以椭圆的几何性质为载体,考查椭圆的标准方程,考查直线与椭圆的位置关系,同时考查向量与解析几何的交汇,综合性强.

练习册系列答案
相关题目

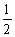

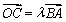

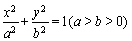


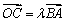
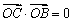
 ,过左焦点F(-1,0)作直线l与椭圆交于点P,Q,直线AP,AQ分别与直线x=-4交于点M,N.
,过左焦点F(-1,0)作直线l与椭圆交于点P,Q,直线AP,AQ分别与直线x=-4交于点M,N.