题目内容
如图，已知椭圆
的右顶点为A（2，0），点P（2e，
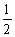）在椭圆上（e为椭圆的离心率）．
（1）求椭圆的方程；
（2）若点B，C（C在第一象限）都在椭圆上，满足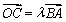
，且
，求实数λ的值．
【答案】
（1）
，（2）
.
【解析】
试题分析：（1）求椭圆方程，基本方法是待定系数法.关键是找全所需条件. 椭圆中
三个未知数的确定只需两个独立条件，本题椭圆经过两点，就是两个独立条件，（2）直线与椭圆位置关系问题就要从其位置关系出发，本题中
和
条件一是平行关系，二是垂直关系.设直线
的斜率就可表示点
及点
再利用就可列出关于斜率及λ的方程组.得到
，可利用类比得到
由
两式相除可解得
代入可得
试题解析：（1）由条件，
代入椭圆方程，
得
2分网]椭
所以椭圆的方程为
5分
（2）设直线OC的斜率为
，
则直线OC方程为
，
代入椭圆方程
即
，
得
则
7分
又直线AB方程为
代入椭圆方程
得
则
9分
在第一象限，
12分
由
得
15分
16分
考点：椭圆方程，直线与椭圆位置关系.
练习册系列答案
全能测控期末小状元系列答案
智趣暑假温故知新系列答案
相关题目
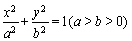
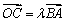
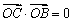
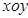中，如图，已知椭圆
的左右顶点为A,B，右顶点为F，设过点T（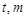
）的直线TA,TB与椭圆分别交于点M
，
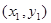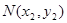，其中m>0,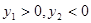
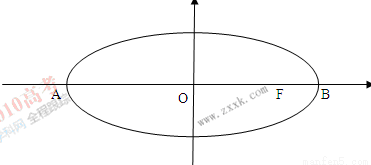
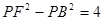,求点P的轨迹
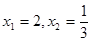，求点T的坐标
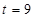,求证：直线MN必过x轴上的一定点
中，如图，已知椭圆
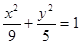的左右顶点为A,B，右顶点为F，设过点T（
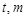）的直线TA,TB与椭圆分别交于点M
，
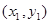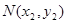，其中m>0,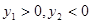
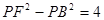,求点P的轨迹
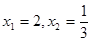，求点T的坐标
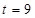,求证：直线MN必过x轴上的一定点
的右焦点为F，过F的直线（非x轴）交椭圆于M、N两点，右准线
交x轴于点K，左顶点为A． 
，试用