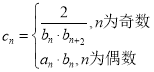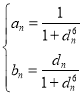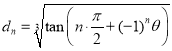题目内容
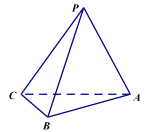
【题目】已知椭圆
：
的离心率为
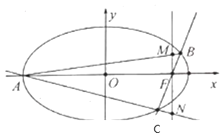
，点A为该椭圆的左顶点，过右焦点
的直线l与椭圆交于B，C两点，当
轴时，三角形ABC的面积为18．
求椭圆的方程；
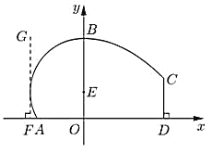
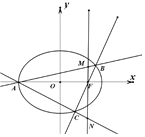
如图，当动直线BC斜率存在且不为0时，直线
分别交直线AB，AC于点M、N，问x轴上是否存在点P，使得
，若存在求出点P的坐标；若不存在说明理由．
【答案】
； 
存在，P
或
.
【解析】
由离心率及三角形ABC的面积和a，b，c之间的关系求出椭圆方程；
由知A的坐标，设直线BC的方程，及B，C的坐标，进而写直线AB，AC的方程，与直线
联立求出M，N的坐标，假设存在P点，是
，使
，求出P点坐标．
解：由已知条件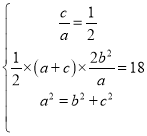得
，解得
；
所以椭圆
的方程为
；
设动直线BC的方程为
，
，
，
则直线AB、AC的方程分别为
和
，
所以点M、N的坐标分别为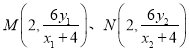
，
联立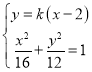
得
，
所以
；
于是
，
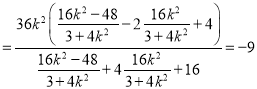假设存在点
满足，则
，所以
或5，
所以当点P为或时，有．
练习册系列答案
相关题目
