题目内容

把抛物线y²=x绕焦点F按顺时针方向旋转45°，设此时抛物线上的最高点为P，则|PF|=________．

$\text{[math]}$
分析：旋转过后，过P的切线斜率为0，旋转之前，过P的切线斜率为1，由此建立方程求出旋转前点的最高点的斜率．
解答：旋转过后，过P的切线斜率为0，旋转之前，过P的切线斜率为1，
∵y²=x
∴2yy′=1
∴y′= $\text{[math]}$
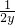
令y′= 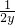$\text{[math]}$ =1
解得y= $\text{[math]}$ ，可得上点的横坐标为 $\text{[math]}$ ，又抛物线y²=x的准线方程是x=- $\text{[math]}$
故|PF|= $\text{[math]}$ + $\text{[math]}$ = $\text{[math]}$ ，
故答案为： $\text{[math]}$ ．
点评：本题考查抛物线的应用，解题本题，关键是由旋转的条件得出旋转前切点的斜率是1，由此利用抛物线的定义求出值，熟记一些相关的结论对解题很方便．