题目内容
已知二次函数y=2x2+3x+1，x∈[-1，2]，则其值域为________．
[
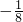，15]
分析：先配方，确定函数的单调性，从而可得函数的最值，即可求得函数的值域．
解答：y=2x2+3x+1=2（x+
）2-
∵x∈[-1，2]，
∴函数在[-1，-）上单调递减，在（-，2]上单调递增
∴x=-时，函数取得最小值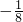；x=2时，函数取得最大值为15
故答案为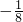：[，15]．
点评：本题考查函数的最值，考查配方法的运用，属于基础题．
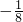，15]分析：先配方，确定函数的单调性，从而可得函数的最值，即可求得函数的值域．
解答：y=2x2+3x+1=2（x+
）2-∵x∈[-1，2]，
∴函数在[-1，-
）上单调递减，在（-，2]上单调递增∴x=-
时，函数取得最小值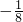；x=2时，函数取得最大值为15故答案为：[
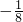，15]．点评：本题考查函数的最值，考查配方法的运用，属于基础题．
练习册系列答案
相关题目