Question

椭圆ax²+by²=1与直线x+y-1=0相交于A、B,C是AB的中点,若|AB|=2,OC的斜率为,求椭圆的方程.

Answer 1

解法一:设A(x₁,y₁)、B(x₂,y₂),代入椭圆方程并作差得a(x₁+x₂)(x₁-x₂)+b(y₁+y₂)(y₁-y₂)=0.?

而,=k_OC=,?

代入上式可得b=a.?

再由|AB|=|x₂-x₁|=2,其中x₁、x₂是方程(a+b)x²-2bx+b-1=0的两根,?

故()²-4·=4,?

将b=a代入得a=,?

∴b=.?

∴所求椭圆的方程是x²+y²=3.

解法二:由?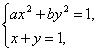

得(a+b)x²-2bx+b-1=0.设A(x₁,y₁)、B(x₂,y₂),?

则???

∵|AB|=2,∴.①?

设C(x,y),则x==,y=1-x=,?

∵OC的斜率为,∴=.?

代入①,得a=,b=.?

∴椭圆方程为.

点评:解法一利用了设点代入、作差,借助斜率的解题方法,称作“差点法”,解法二是圆锥曲线弦长的基本求法,是利用两点间的距离公式求得.