题目内容
已知等差数列{an}满足a2=3,Sn-Sn-3=51(n>3) ,Sn= 100,则n的值为
| A.8 | B.9 | C.10 | D.11 |
C
解析试题分析:根据题意可知,由于等差数列{  },
},
联立方程组得到n=10,故选C.
考点:本试题考查了等差数列的通项公式和前n项和的知识点。
点评:解决该试题的关键是结合数列的通项公式与前n项和的关系的运用,以及熟练的运用前n项和公式和通项公式来求解得到结论,属于基础题。

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
已知Sn是等差数列{an}(nÎN*)的前n项和,且S6>S7>S5,有下列四个命题,假命题的是( )
| A.公差d<0 | B.在所有Sn<0中,S13最大 |
| C.满足Sn>0的n的个数有11个 | D.a6>a7 |
在等差数列{an}中,已知a4+a8=16,则该数列前11项和S11=( )
| A.58 | B.88 | C.143 | D.176 |
已知等差数列 的前
的前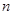 项和为
项和为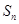 ,且满足
,且满足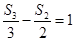 ,则数列
,则数列 的公差是( )
的公差是( )
A. | B.1 | C.2 | D.3 |
若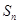 是等差数列
是等差数列 的前n项和,
的前n项和,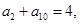 则
则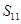 的值为( )
的值为( )
| A.12 | B.22 | C.18 | D.44 |
等差数列 中,a3+a11="8," 数列
中,a3+a11="8," 数列 是等比数列,且b7=a7,则b6b8的值为
是等比数列,且b7=a7,则b6b8的值为
| A.2 | B.4 | C.8 | D.16 |
若 为等差数列
为等差数列 的前n项和,
的前n项和, ,
,  ,则
,则 与
与 的等比中项为( )
的等比中项为( )
A. | B. | C. | D. |
在△ABC中,tanA是以 为第3项,4为第7项的等差数列的公差;tanB是以
为第3项,4为第7项的等差数列的公差;tanB是以 为第3
为第3
项,9为第6项的等比数列的公比,则该三角形为 ( )
| A.等腰三角形 | B.锐角三角形 |
| C.直角三角形 | D.钝角三角形 |
已知等差数列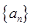 的通项公式
的通项公式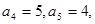 ,则
,则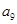 等于( )
等于( )
| A.1 | B.2 | C.0 | D.3 |