题目内容
已知椭圆![]()
![]()
![]() ,求点Q的轨迹方程,并说明轨迹是什么曲线。
,求点Q的轨迹方程,并说明轨迹是什么曲线。
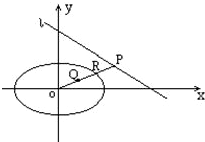
设点P、Q、R的坐标分别为(12, yP),(x, y),(xR,yR),由题设知xR>0,x>0.
|
|
由点R在椭圆上及O、Q、R共线,得方程组:
|
|
| ?? |
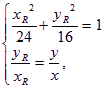 ??
??
由O、Q、P三点共线,得![]()
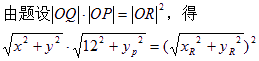
将??????代入上式,整理得点Q的轨迹方程为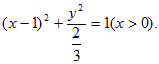
所以,点Q的轨迹是以(1,0)为中心,长、短半轴长分别为1和![]() ,且长轴在x轴上的椭圆,去掉原点。
,且长轴在x轴上的椭圆,去掉原点。
解析:
如上图,动点Q的运动与点P、点R相关连,点P在直线l上,点R在椭圆上,设点Q的坐标为(x, y),利用已知条件将点P、点R的坐标表示出来,再由轨迹条件![]()

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目

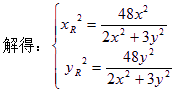
 已知椭圆
已知椭圆