题目内容
(2011•东城区一模)已知数列{an}满足:a1=1,a2=2,a3=3,a4=4,a5=5,且当n≥5时,an+1=a1a2…an-1,若数列{bn}满足对任意n∈N*,有bn=a1a2…an-a12-a22-…-an2,则b5=
65
65
;当n≥5时,bn=70-n
70-n
.分析:在bn=a1a2…an-a12-a22-…-an2中,令n=5代入数据计算即可求出b5.由bn=a1a2…an-a12-a22-…-an2中构造出bn+1=a1a2…anan+1-a12-a22-…-an2-an+12,两式相减,并化简整理,可以判断出当n≥5时,数列{bn}的各项组成等差数列.利用等差数列通项公式求解即可.
解答:解:由已知,b5=a1a2…a5-a12-a22-…-a52
=1×2×3×4×5-(12+22+32+42+52)
=120-55
=65.
当n≥5时,由an+1=a1a2…an-1,移向得出a1a2…an-1=an+1+1 ①
∵bn=a1a2…an-a12-a22-…-an2,②
∴bn+1=a1a2…anan+1-a12-a22-…-an2-an+12 ③
③-②得bn+1-bn=a1a2…anan+1-a1a2…an-an+12
=a1a2…an(an+1-1)-an+12 (将①式代入)
=(an+1+1)(an+1-1)-an+12=an+12-1-an+12
=-1
∴当n≥5时,数列{bn}的各项组成等差数列,
∴bn=b5+(n-5)×(-1)=65-(n-5)=70-n.
故答案为:65 70-n
=1×2×3×4×5-(12+22+32+42+52)
=120-55
=65.
当n≥5时,由an+1=a1a2…an-1,移向得出a1a2…an-1=an+1+1 ①
∵bn=a1a2…an-a12-a22-…-an2,②
∴bn+1=a1a2…anan+1-a12-a22-…-an2-an+12 ③
③-②得bn+1-bn=a1a2…anan+1-a1a2…an-an+12
=a1a2…an(an+1-1)-an+12 (将①式代入)
=(an+1+1)(an+1-1)-an+12=an+12-1-an+12
=-1
∴当n≥5时,数列{bn}的各项组成等差数列,
∴bn=b5+(n-5)×(-1)=65-(n-5)=70-n.
故答案为:65 70-n
点评:本题考查等差关系的判定、通项公式.考查转化、变形构造、计算能力.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
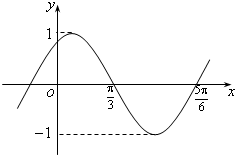 (2011•东城区一模)已知函数y=sin(ωx+φ)
(2011•东城区一模)已知函数y=sin(ωx+φ)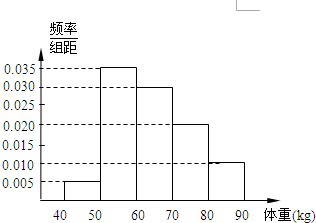 (2011•东城区一模)从某地高中男生中随机抽取100名同学,将他们的体重(单位:kg)数据绘制成频率分布直方图(如图).由图中数据可知体重的平均值为
(2011•东城区一模)从某地高中男生中随机抽取100名同学,将他们的体重(单位:kg)数据绘制成频率分布直方图(如图).由图中数据可知体重的平均值为