题目内容
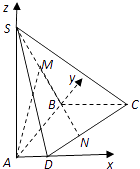
【题目】如图,在四棱锥S﹣ABCD中,底面ABCD是直角梯形,侧棱SA⊥底面ABCD,AB垂直于AD和BC,SA=AB=BC=2,AD=1.M是棱SB的中点. (Ⅰ)求证:AM∥面SCD;
(Ⅱ)求面SCD与面SAB所成二面角的余弦值;
(Ⅲ)设点N是直线CD上的动点,MN与面SAB所成的角为θ,求sinθ的最大值.
【答案】解:(Ⅰ)以点A为原点建立如图所示的空间直角坐标系,则 A(0,0,0),B(0,2,0),D(1,0,0,),S(0,0,2),M(0,1,1).
则 ![]() ,
, ![]() ,
, ![]() .
.
设平面SCD的法向量是 ![]() ,则
,则 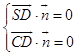 ,即
,即 ![]()
令z=1,则x=2,y=﹣1.于是 ![]() .
.
∵ ![]() ,∴
,∴ ![]() .
.
又∵AM平面SCD,∴AM∥平面SCD.
(Ⅱ)易知平面SAB的法向量为 ![]() .设平面SCD与平面SAB所成的二面角为α,
.设平面SCD与平面SAB所成的二面角为α,
则 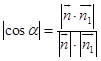 =
= ![]() =
= ![]() ,即
,即 ![]() .
.
∴平面SCD与平面SAB所成二面角的余弦值为 ![]() .
.
(Ⅲ)设N(x,2x﹣2,0),则 ![]() .
.
∴ 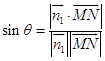 =
= ![]() =
=  =
= 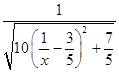 .
.
当 ![]() ,即
,即 ![]() 时,
时, ![]() .
.
【解析】(Ⅰ)通过建立空间直角坐标系,利用平面SCD的法向量 ![]() 即可证明AM∥平面SCD;(Ⅱ)分别求出平面SCD与平面SAB的法向量,利用法向量的夹角即可得出;(Ⅲ)利用线面角的夹角公式即可得出表达式,进而利用二次函数的单调性即可得出.
即可证明AM∥平面SCD;(Ⅱ)分别求出平面SCD与平面SAB的法向量,利用法向量的夹角即可得出;(Ⅲ)利用线面角的夹角公式即可得出表达式,进而利用二次函数的单调性即可得出.
【考点精析】关于本题考查的直线与平面平行的判定和空间角的异面直线所成的角,需要了解平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线平行;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则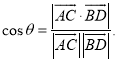 才能得出正确答案.
才能得出正确答案.

练习册系列答案
相关题目


