题目内容
在直角坐标平面内,曲线C的参数方程为
(α为参数),经过变换
后曲线C变换为曲线C′
(1)以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,求曲线C′的极坐标方程;
(2)求证:直线x-
y-2=0与曲线C'的交点在曲线C上.
|
|
(1)以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,求曲线C′的极坐标方程;
(2)求证:直线x-
| 2 |
分析:(1)把曲线C的参数方程代入变换式
,再消去参数α即可得到曲线C′;
(2)联立直线与曲线C'的方程,解得交点,代入曲线C的方程看是否成立即可得出答案.
|
(2)联立直线与曲线C'的方程,解得交点,代入曲线C的方程看是否成立即可得出答案.
解答:解:(1)把曲线C的参数方程为
(α为参数),代入经过变换
后得
,消去参数α得曲线C':(X-1)2+Y2=1,
即曲线C′是以(1,0)为圆心,1为半径的圆,故其极坐标方程为ρ=2cosθ.
(2)联立得
,解得
或
,即两交点为(2,0),(
,-
).
由曲线C的参数方程
(α为参数),消去参数α得
+y2=1.
把两交点为(2,0),(
,-
)代入上述方程得:
+0=1,
+(-
)2=1,
可知该两点均在曲线C上.
|
|
后得
|
即曲线C′是以(1,0)为圆心,1为半径的圆,故其极坐标方程为ρ=2cosθ.
(2)联立得
|
|
|
| 2 |
| 3 |
2
| ||
| 3 |
由曲线C的参数方程
|
| x2 |
| 4 |
把两交点为(2,0),(
| 2 |
| 3 |
2
| ||
| 3 |
| x2 |
| 4 |
(
| ||
| 4 |
2
| ||
| 3 |
可知该两点均在曲线C上.
点评:正确理解变换和方程组的解与曲线的交点之间的关系是解题的关键.

练习册系列答案
相关题目
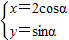 (α为参数),经过变换
(α为参数),经过变换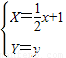 后曲线C变换为曲线C′
后曲线C变换为曲线C′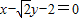 与曲线C'的交点在曲线C上.
与曲线C'的交点在曲线C上.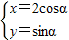 (α为参数),经过变换
(α为参数),经过变换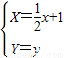 后曲线C变换为曲线C′
后曲线C变换为曲线C′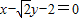 与曲线C'的交点在曲线C上.
与曲线C'的交点在曲线C上.