题目内容
设椭圆 +
+ =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,短轴一个端点到右焦点的距离为2.
,短轴一个端点到右焦点的距离为2.
(1)求椭圆的方程.
(2)若P是该椭圆上的一个动点,F1、F2分别是椭圆的左、右焦点,求 的最大值和最小值.
的最大值和最小值.
解:(1)设所求的椭圆方程为  (a>b>0),
(a>b>0),
由离心率e= =
=
则 解得a=2,b=1,c=
解得a=2,b=1,c=
故所求椭圆的方程为 ,
,
(2)由(1)知F1(- ,0),设P(x,y),
,0),设P(x,y),
则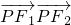 =(-
=(- -x,-y)•(
-x,-y)•(  -x,-y)=x2+y2-3=
-x,-y)=x2+y2-3= (3x2-8)
(3x2-8)
∵x∈[-2,2],∴0≤x2≤4,
故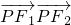 ∈[-2,1]
∈[-2,1]
故最大值1,最小值-2.
分析:(1)先设出椭圆的标准方程,进而根据焦点坐标确定c,根据焦点于长轴上较近的端点距离确定a,进而根据a,b和c的关系确定b,椭圆方程可得.
(2)设出点P的坐标,进而可表示出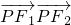 ,进而根据x的范围确定
,进而根据x的范围确定 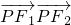 的范围
的范围
点评:本题主要考查了椭圆的应用.解答的关键是利用待定系数法求椭圆方程及平面向量的基本计算.
 (a>b>0),
(a>b>0),由离心率e=
 =
=
则
 解得a=2,b=1,c=
解得a=2,b=1,c=
故所求椭圆的方程为
 ,
,(2)由(1)知F1(-
 ,0),设P(x,y),
,0),设P(x,y),则
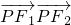 =(-
=(- -x,-y)•(
-x,-y)•(  -x,-y)=x2+y2-3=
-x,-y)=x2+y2-3= (3x2-8)
(3x2-8)∵x∈[-2,2],∴0≤x2≤4,
故
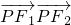 ∈[-2,1]
∈[-2,1]故最大值1,最小值-2.
分析:(1)先设出椭圆的标准方程,进而根据焦点坐标确定c,根据焦点于长轴上较近的端点距离确定a,进而根据a,b和c的关系确定b,椭圆方程可得.
(2)设出点P的坐标,进而可表示出
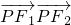 ,进而根据x的范围确定
,进而根据x的范围确定 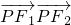 的范围
的范围点评:本题主要考查了椭圆的应用.解答的关键是利用待定系数法求椭圆方程及平面向量的基本计算.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 =1(a>b>0)的左、右焦点分别为F1,F2,A是椭圆上的一点,AF2⊥F1F2,原点O到直线AF1的距离为
=1(a>b>0)的左、右焦点分别为F1,F2,A是椭圆上的一点,AF2⊥F1F2,原点O到直线AF1的距离为 .
. ;
; =λ1
=λ1 ,
,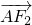 =λ2
=λ2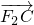 ,当A在椭圆上运动时,求证:λ1+λ2为定值.
,当A在椭圆上运动时,求证:λ1+λ2为定值.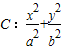 =1(a>b>0)过点
=1(a>b>0)过点 ,且左焦点为
,且左焦点为
 •
•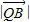 =
=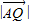 •
• ,证明:点Q总在某定直线上.
,证明:点Q总在某定直线上. =1(a>b>0)过点
=1(a>b>0)过点 ,且左焦点为
,且左焦点为
 •
• =
= •
• ,证明:点Q总在某定直线上.
,证明:点Q总在某定直线上. =1(a>b>0)的焦距为2c.以点O为圆心,a为半径作圆M.若过点P(
=1(a>b>0)的焦距为2c.以点O为圆心,a为半径作圆M.若过点P( ,0)所作圆M的两条切线互相垂直,则该椭圆的离心率为______
,0)所作圆M的两条切线互相垂直,则该椭圆的离心率为______