题目内容
设椭圆 +
+ =1(a>b>0)的离心率为e,A为椭圆上一点,弦AB,AC分别过焦点F1,F2.
=1(a>b>0)的离心率为e,A为椭圆上一点,弦AB,AC分别过焦点F1,F2.
(I)若∠AF1F2=α,∠AF2F1=β,试用α,β表示椭圆的离心率e;
(II)设 =λ1
=λ1 ,
,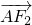 =λ2
=λ2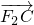 ,当A在椭圆上运动时,求证:λ1+λ2为定值.
,当A在椭圆上运动时,求证:λ1+λ2为定值.
 解:(I)设F1(-c,0),F2(c,0).在△AF1F2中,由正弦定理得
解:(I)设F1(-c,0),F2(c,0).在△AF1F2中,由正弦定理得 =
= =
= ,
,即|AF1|=
 ,|AF2|=
,|AF2|= ,
,所以2a=|AF1|+|AF2|=
 +
+ ,
,=2c(
 +
+ )=2c•
)=2c• ,
,得e=
 .
.(II)设A(x0,y0),B(x1,y1),C(x2,y2).
①当y0=0时,λ1+λ2=2
 =
= ;当AB或AC与x轴垂直时,λ1+λ2=
;当AB或AC与x轴垂直时,λ1+λ2= .
.②当AB,AC都不与x轴垂直且y0≠0时,AC的方程为y=
 (x-c),
(x-c),由
 ,
,消x得[b2(x0-c)2+a2y02]y2+2b2y0(x0-c)y+c2b2y02-a2b2y02=0.
由韦达定理得 y2y0=
 ,
,所以y2=
 ,
,所以 λ2=
 =-
=- =-
=- ,
,同理可得λ1=
 =-
=- =-
=- ,
,故λ1+λ2=
 .
.分析:(I)设F1(-c,0),F2(c,0).在△AF1F2中,由正弦定理得
 =
= =
= ,由此能求出e=
,由此能求出e= .
.(II)设A(x0,y0),B(x1,y1),C(x2,y2).当y0=0时,λ1+λ2=2
 =
= ;当AB或AC与x轴垂直时,λ1+λ2=
;当AB或AC与x轴垂直时,λ1+λ2= ..当AB,AC都不与x轴垂直且y0≠0时,AC的方程为y=
..当AB,AC都不与x轴垂直且y0≠0时,AC的方程为y= (x-c),由此能证明λ1+λ2=
(x-c),由此能证明λ1+λ2= .
.点评:本题主要考查椭圆标准方程,简单几何性质,直线与椭圆的位置关系,椭圆的简单性质等基础知识.考查运算求解能力,推理论证能力;考查函数与方程思想,化归与转化思想.

练习册系列答案
相关题目
 =1(a>b>0)的左、右焦点分别为F1,F2,A是椭圆上的一点,AF2⊥F1F2,原点O到直线AF1的距离为
=1(a>b>0)的左、右焦点分别为F1,F2,A是椭圆上的一点,AF2⊥F1F2,原点O到直线AF1的距离为 .
. ;
;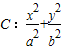 =1(a>b>0)过点
=1(a>b>0)过点 ,且左焦点为
,且左焦点为
 •
•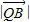 =
=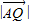 •
• ,证明:点Q总在某定直线上.
,证明:点Q总在某定直线上. =1(a>b>0)过点
=1(a>b>0)过点 ,且左焦点为
,且左焦点为
 •
• =
= •
• ,证明:点Q总在某定直线上.
,证明:点Q总在某定直线上. =1(a>b>0)的焦距为2c.以点O为圆心,a为半径作圆M.若过点P(
=1(a>b>0)的焦距为2c.以点O为圆心,a为半径作圆M.若过点P( ,0)所作圆M的两条切线互相垂直,则该椭圆的离心率为______
,0)所作圆M的两条切线互相垂直,则该椭圆的离心率为______