题目内容
2.某商店计划每天购进某商品若干千件,商店每销售一件该商品可获利涧50元,供大于求时,剩余商品全部退回,但每件商品亏损10元;若供不应求,则从外徘调剂,此时每件调剂商品可获利30元.(1)若商店一天购进该商品10件,求当天的利润y(单位:元)关于当天需求量n(单位:件,n∈N*)的函数解析式;
(2)商店记录了50天该商品的日需求量n(单位:件).整理得下表:
| 日需求量 | 8 | 9 | 10 | 11 | 12 |
| 频数 | 9 | 11 | 15 | 10 | 5 |
分析 (1)根据题意分段求解得出当1≤n≤10时,y利润,当n>10时,y利润,由此能求出当天的利润y(单位:元)关于当天需求量n(单位:件,n∈N)的函数解析式.
(2)由已知得X的可能取值为380,440,500,530,560,分别求出相应的概率,由此能求出X的分布列和平均值.
解答 解:(1)当1≤n≤10时,y利润=50n+(10-n)×(-10)=60n-100,
当n>10时,y利润=50×10+(n-10)×30=30n+200,
所以函数解析式y利润=$\left\{\begin{array}{l}{30n+200,n>10}\\{6n-100,1≤n≤10}\end{array}\right.$.
(2)∵日需求量为8,频数9天,利润为50×8-10×2=380,
日需求量为9,频数11天,利润为50×9-10×1=440,
日需求量为10,频数15,利润为50×10=500,
日需求量为11,频数10,利润为50×10+30=530,
日需求量为12,频数5,利润为50×10+30×2=560,
∴X的可能取值为380,440,500,530,560,
P(X=380)=$\frac{9}{50}$,P(X=440)=$\frac{11}{50}$,P(X=500)=$\frac{15}{50}$,P(X=530)=$\frac{10}{50}$,P(X=560)=$\frac{5}{50}$,
∴X的分布列为:
| X | 380 | 440 | 500 | 530 | 560 |
| P | $\frac{9}{50}$ | $\frac{11}{50}$ | $\frac{15}{50}$ | $\frac{10}{50}$ | $\frac{5}{50}$ |
点评 本题考查了运用概率知识求解实际问题的利润问题,考查离散型随机变量的分布列和数学期望,考查利用数学知识解决实际问题,考查学生的计算能力,属于中档题

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
12.复数z满足(1+i)z=2i(i为虚数单位),则z在复平面内对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
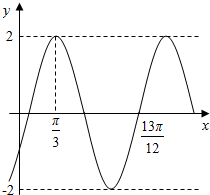 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$,x∈R)的部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$,x∈R)的部分图象如图所示.