题目内容
(本小题满分12分)
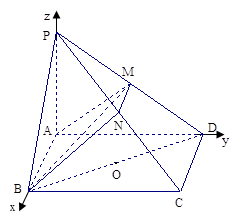
如图,在四棱锥 中,底面
中,底面 是矩形,
是矩形, 平面
平面 ,
, ,
, ,点
,点 为
为 的中点,
的中点, 为
为 中点.
中点.
(1)求证:平面 ⊥平面
⊥平面 ;
;
(2)求直线 与平面
与平面 所成的角的正弦值;
所成的角的正弦值;
(3)求点 到平面
到平面 的距离.
的距离.
(1)证明:见解析;(2)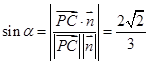 ;(3)
;(3)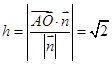 。
。
解析试题分析:(I)根据面面垂直的判定定理,证明:PD⊥平面ABM即可.
(II)本小题易建立直角坐标系,然后利用向量法求解,设平面ABM的法向量 ,
,
则 求解即可.
求解即可.
(III) 设所求距离为h,利用 求距离即可.
求距离即可.
(1)证明: 因为  ,
, 为
为 中点 , 所以 AM⊥PD.
中点 , 所以 AM⊥PD.
因为PA⊥平面ABCD,则PA⊥AB,又AB⊥AD,
所以AB⊥平面PAD,则AB⊥PD,因此有PD⊥平面ABM,
所以平面ABM⊥平面PCD. ------------ 4 分
(向量法也可)
(2)如图所示,建立空间直角坐标系,则 ,
, ,
,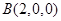 ,
,  ,
, ,
, ,
,
设平面 的一个法向量
的一个法向量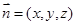 ,由
,由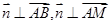 可得:
可得: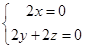 ,令
,令 ,则
,则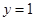 ,即
,即 .
.
设所求角为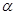 ,则
,则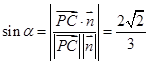 , ------------ 8 分
, ------------ 8 分
(3)设所求距离为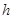 ,由
,由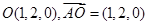 ,
,
得: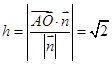 ---------------------- 12分
---------------------- 12分
考点:线面垂直,面面垂直的判定与性质,直线与平面所成的角,点O到平面的距离.
点评:掌握线线,线面,面面垂直的判定与性质,直线与平面所成的角的定义,点到平面的距离的常见求法是求解此类问题的基础.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
 ABC=60
ABC=60 ,EC
,EC 面ABCD,FA
面ABCD,FA
 中,
中, 平面
平面 ,
, ,
, ,
, .
. ;
; 的正弦值;
的正弦值; 为棱
为棱 上的点,满足异面直线
上的点,满足异面直线 与
与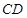 所成的角为
所成的角为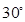 ,求
,求 的长.
的长.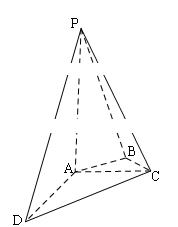
 与直角梯形
与直角梯形 垂直,
垂直, ,
, ,
, ,
, .若
.若 分别为
分别为 的中点.(1)求
的中点.(1)求 的值; (2)求面
的值; (2)求面 与面
与面 所成的二面角大小.
所成的二面角大小.

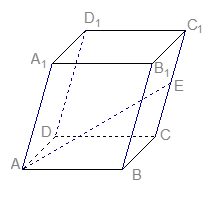
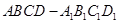 中,
中,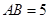 ,
,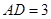 ,
,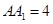 ,
,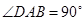 ,
,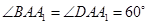 ,
, 是
是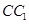 的中点,设
的中点,设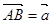 ,
,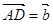 ,
, .
.
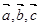 表示
表示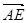 ;
; 的长.
的长. ∩平面
∩平面 =AB,PQ⊥
=AB,PQ⊥
 被一平面所截,截面
被一平面所截,截面 是一个平行四边形.求证:
是一个平行四边形.求证: ;
;
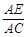 =
= =λ (0<λ<1).
=λ (0<λ<1).