题目内容
已知函数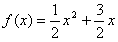 ,数列{an}的前n项和为Sn,点(n,Sn)(n∈N*)均在函数y=f(x)的图象上,
,数列{an}的前n项和为Sn,点(n,Sn)(n∈N*)均在函数y=f(x)的图象上,
(Ⅰ)求数列{an}的通项公式an;
(Ⅱ)令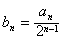 ,求数列{bn}的前n项和为Tn;
,求数列{bn}的前n项和为Tn;
(Ⅲ)令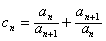 ,证明:2n<c1+c2+…+cn<2n+
,证明:2n<c1+c2+…+cn<2n+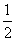 。
。
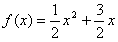 ,数列{an}的前n项和为Sn,点(n,Sn)(n∈N*)均在函数y=f(x)的图象上,
,数列{an}的前n项和为Sn,点(n,Sn)(n∈N*)均在函数y=f(x)的图象上,(Ⅰ)求数列{an}的通项公式an;
(Ⅱ)令
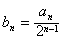 ,求数列{bn}的前n项和为Tn;
,求数列{bn}的前n项和为Tn;(Ⅲ)令
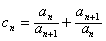 ,证明:2n<c1+c2+…+cn<2n+
,证明:2n<c1+c2+…+cn<2n+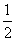 。
。 (Ⅰ)解:∵点(n,Sn)在f(x)的图象上,
∴ ,
,
当n≥2时, ,
,
当n=1时,a1=S1=2符合上式,
∴an=n+1(n∈N*);
(Ⅱ)解: ,
,


由①-②,得


 ,
,
∴ ;
;
(Ⅲ)证明:由 ,
,
∴c1+c2+cn+…+cn>2n,
又 ,
,
∴c1+c2+…+cn

 ,
,
∴2n<c1+c2+…+cn< 成立。
成立。
∴
 ,
,当n≥2时,
 ,
,当n=1时,a1=S1=2符合上式,
∴an=n+1(n∈N*);
(Ⅱ)解:
 ,
,

由①-②,得


 ,
,∴
 ;
;(Ⅲ)证明:由
 ,
, ∴c1+c2+cn+…+cn>2n,
又
 ,
, ∴c1+c2+…+cn

 ,
,∴2n<c1+c2+…+cn<
 成立。
成立。
练习册系列答案
相关题目
 ,数列an满足
,数列an满足 .
.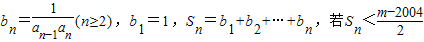 对一切n∈N*成立,求最小正整数m.
对一切n∈N*成立,求最小正整数m.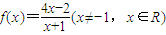 ,数列{an}满足 a1=a(a≠-1,a∈R),an+1=f(an)(n∈N*).
,数列{an}满足 a1=a(a≠-1,a∈R),an+1=f(an)(n∈N*). ,证明数列{bn}是等比数列,并求出通项公式an.
,证明数列{bn}是等比数列,并求出通项公式an. 若数列{an}满足an=
若数列{an}满足an= (n∈N+)且{an}是递减数列,则实数a的取值范围是( )
(n∈N+)且{an}是递减数列,则实数a的取值范围是( ) ,1) B.(
,1) B.(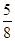 ) C.(
) C.( ) D.(
) D.( ,数列an满足an=f(n)(n∈N*),且an是递增数列,则实数a的取值范围是
,数列an满足an=f(n)(n∈N*),且an是递增数列,则实数a的取值范围是