题目内容
设等差数列{an}的第10项为23,第25项为-22,求:(1)数列{an}的通项公式;
(2)数列{an}前n项的绝对值之和Tn.
【答案】分析:(1)设等差数列{an}的公差为d,利用等差数列的通项公式可知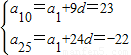 ,解得即可.
,解得即可.
(2)设数列{an}的前n项和为Sn.
由an≥0,解得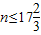 ,an<0,
,an<0,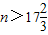 .,所以此数列的前17项均为正数,从第18项开始均为负数.
.,所以此数列的前17项均为正数,从第18项开始均为负数.
所以当n≤17时,利用等差数列的前n项和公式可得Tn=a1+a2+…+an=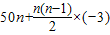 .
.
当n>17时,Tn=T17-(a18+a19+…+an)=S17-(Sn-S17)=2S17-Sn,代入即可.
解答:解:(1)设等差数列{an}的公差为d,由已知可知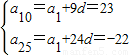 ,解得
,解得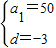 .
.
∴an=50+(n-1)×(-3)=-3n+53.
(2)设数列{an}的前n项和为Sn.
由an≥0,解得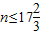 ,an<0,
,an<0,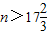 .,所以此数列的前17项均为正数,从第18项开始均为负数.
.,所以此数列的前17项均为正数,从第18项开始均为负数.
所以当n≤17时,Tn=a1+a2+…+an=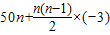 =
=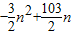 .
.
当n>17时,Tn=T17-(a18+a19+…+an)
=S17-(Sn-S17)
=2S17-Sn
=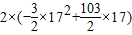 -
-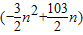
=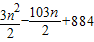 .
.
点评:熟练掌握等差数列的通项公式、前n项和公式以及含绝对值符号的数列求和方法等是解题的关键.
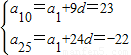 ,解得即可.
,解得即可.(2)设数列{an}的前n项和为Sn.
由an≥0,解得
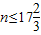 ,an<0,
,an<0,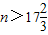 .,所以此数列的前17项均为正数,从第18项开始均为负数.
.,所以此数列的前17项均为正数,从第18项开始均为负数.所以当n≤17时,利用等差数列的前n项和公式可得Tn=a1+a2+…+an=
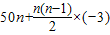 .
.当n>17时,Tn=T17-(a18+a19+…+an)=S17-(Sn-S17)=2S17-Sn,代入即可.
解答:解:(1)设等差数列{an}的公差为d,由已知可知
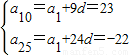 ,解得
,解得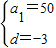 .
.∴an=50+(n-1)×(-3)=-3n+53.
(2)设数列{an}的前n项和为Sn.
由an≥0,解得
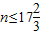 ,an<0,
,an<0,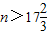 .,所以此数列的前17项均为正数,从第18项开始均为负数.
.,所以此数列的前17项均为正数,从第18项开始均为负数.所以当n≤17时,Tn=a1+a2+…+an=
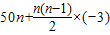 =
=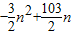 .
.当n>17时,Tn=T17-(a18+a19+…+an)
=S17-(Sn-S17)
=2S17-Sn
=
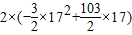 -
-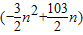
=
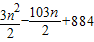 .
.点评:熟练掌握等差数列的通项公式、前n项和公式以及含绝对值符号的数列求和方法等是解题的关键.

练习册系列答案
相关题目