题目内容
已知f(x)=( +
+ )2(x≥0),又数列{an}(an>0)中,a1=2,这个数列的前n项和的公式Sn(n∈N*)对所有大于1的自然数n都有Sn=f(Sn-1).
)2(x≥0),又数列{an}(an>0)中,a1=2,这个数列的前n项和的公式Sn(n∈N*)对所有大于1的自然数n都有Sn=f(Sn-1).
(1)求数列{an}的通项公式;
(2)若bn=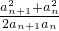 (n∈N*),求证
(n∈N*),求证 (b1+b2+…+bn-n)=1.
(b1+b2+…+bn-n)=1.
解:(1)∵f(x)=( +
+ )2,
)2,
∴Sn=(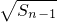 +
+ )2.
)2.
∴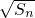 -
-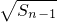 =
= .又
.又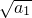 =
= ,
,
故有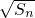 =
= +(n-1)
+(n-1) =n
=n ,
,
即Sn=2n2(n∈N*).
当n≥2时,an=Sn-Sn-1=2n2-2(n-1)2=4n-2;
当n=1时,a1=2,适合an=4n-2.
因此,an=4n-2(n∈N*).
(2)∵bn=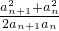 =1+
=1+ -
- ,
,
∴b1+b2+b3++bn-n=1- .
.
从而 (b1+b2++bn-n)=
(b1+b2++bn-n)= (1-
(1- )=1.
)=1.
分析:(1)由于已知条件给出的是Sn与Sn-1的函数关系,而要求的是an的通项公式,故关键是确定Sn.知道Sn后,能够导出数列{an}的通项公式.
(2)由bn=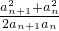 =1+
=1+ -
- ,知b1+b2+b3++bn-n=1-
,知b1+b2+b3++bn-n=1- .从而能够导出
.从而能够导出 (b1+b2+…+bn-n)=1.
(b1+b2+…+bn-n)=1.
点评:本题考查数列的极限及其应用,解题时要注意数列的性质的灵活运用.
 +
+ )2,
)2,∴Sn=(
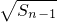 +
+ )2.
)2.∴
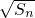 -
-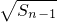 =
= .又
.又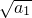 =
= ,
,故有
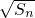 =
= +(n-1)
+(n-1) =n
=n ,
,即Sn=2n2(n∈N*).
当n≥2时,an=Sn-Sn-1=2n2-2(n-1)2=4n-2;
当n=1时,a1=2,适合an=4n-2.
因此,an=4n-2(n∈N*).
(2)∵bn=
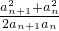 =1+
=1+ -
- ,
,∴b1+b2+b3++bn-n=1-
 .
.从而
 (b1+b2++bn-n)=
(b1+b2++bn-n)= (1-
(1- )=1.
)=1.分析:(1)由于已知条件给出的是Sn与Sn-1的函数关系,而要求的是an的通项公式,故关键是确定Sn.知道Sn后,能够导出数列{an}的通项公式.
(2)由bn=
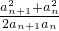 =1+
=1+ -
- ,知b1+b2+b3++bn-n=1-
,知b1+b2+b3++bn-n=1- .从而能够导出
.从而能够导出 (b1+b2+…+bn-n)=1.
(b1+b2+…+bn-n)=1.点评:本题考查数列的极限及其应用,解题时要注意数列的性质的灵活运用.

练习册系列答案
相关题目