题目内容
设 ,
,
(1)当 时,求曲线
时,求曲线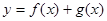 在
在 处的切线方程
处的切线方程
(2)如果对任意的 ,恒有
,恒有 成立,求实数
成立,求实数 的取值范围
的取值范围
【答案】
(1)令 ,则
,则


故 曲线 在
在 处的切线方程为
处的切线方程为  ,
,
即 (4分)
(4分)
(2) ,令
,令
而 ,故
,故 在
在 上
上 (6分)
(6分)
 在
在 上恒成立
上恒成立
 在
在 上恒成立
上恒成立
即 在
在 上恒成立
上恒成立
 在
在 上恒成立 (7分)
上恒成立 (7分)
记
 ,则
,则 (8分)
(8分)
下证明 在
在 上是单调减的
上是单调减的
【 记 ,
, 在
在 上是单调减的
上是单调减的

因此, 在
在 上是单调减的
上是单调减的
在 上是单调减的】
(11分)
上是单调减的】
(11分)

 在
在 内有且只有一个零点,即为
内有且只有一个零点,即为
当 时,
时,
 是增的
是增的
当 时,
时,
 是减的
是减的
故  时,
时,
 ,即
,即
【解析】(1)求导,代入得;(2)任意的 ,恒有
,恒有 成立,得
成立,得

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
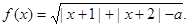
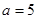 时,求函数
时,求函数 的定义域;
的定义域; 的取值范围.
的取值范围.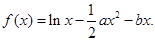 (1)当
(1)当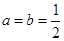 时,求
时,求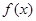 的最大值;(2)令
的最大值;(2)令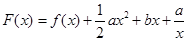 ,(
,(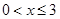 ),其图象上任意一点
),其图象上任意一点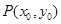 处切线的斜率
处切线的斜率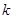 ≤
≤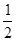 恒成立,求实数
恒成立,求实数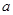 的取值范围;(3)当
的取值范围;(3)当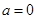 ,
,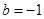 ,方程
,方程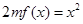 有唯一实数解,求正数
有唯一实数解,求正数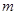 的值.
的值.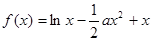
 时,求
时,求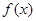 的最大值;
的最大值;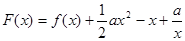
 ,以其图象上任意一点
,以其图象上任意一点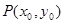 为切点的切线的斜率
为切点的切线的斜率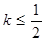 恒成立,求实数
恒成立,求实数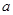 的取值范围;
的取值范围;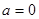 时,方程
时,方程 有唯一实数解,求正数
有唯一实数解,求正数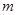 的值.
的值. .
. 时,求函数
时,求函数 在区间
在区间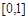 上的最小值;
上的最小值; 时,曲线
时,曲线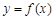 在点
在点 处的切线为
处的切线为 ,
,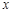 轴交于点
轴交于点
 .
.
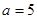 时,求函数
时,求函数 的定义域;
的定义域;  的取值范围。
的取值范围。