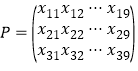题目内容
【题目】已知椭圆E的一个顶点为![]() ,焦点在x轴上,若椭圆的右焦点到直线
,焦点在x轴上,若椭圆的右焦点到直线![]() 的距离是3.
的距离是3.
![]() 求椭圆E的方程;
求椭圆E的方程;
![]() 设过点A的直线l与该椭圆交于另一点B,当弦AB的长度最大时,求直线l的方程.
设过点A的直线l与该椭圆交于另一点B,当弦AB的长度最大时,求直线l的方程.
【答案】(1)![]() (2)
(2)![]() 或
或![]()
【解析】
(1)根据点到直线的距离列式求得c,再求得a;
(2)根据弦长公式求得弦长后,换元成二次函数求最值.
(1)由题意,![]()
右焦点![]() 到直线
到直线![]() 的距离
的距离![]() ,
,![]() ,
,
![]() ,
,
∵椭圆![]() 的焦点在
的焦点在![]() 轴上,所以椭圆
轴上,所以椭圆![]() 的方程为
的方程为![]()
(2)〖解法1〗当![]() 不存在时,
不存在时,![]()
当![]() 存在时,设直线方程为
存在时,设直线方程为![]() ,联立
,联立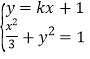 ,得
,得![]() ,
,
![]()
![]()
令![]() 则
则![]()
所以,当![]() ,即
,即![]() ,得
,得![]() 时
时
![]() 的最大值为
的最大值为![]() ,即
,即![]() 的最大值为
的最大值为![]()
直线的方程为![]() .
.
(2)〖解法2〗设直线![]() 的倾斜角为
的倾斜角为![]() ,则直线
,则直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),
为参数),
设![]() 点对应的参数分别为
点对应的参数分别为![]() ,且
,且![]() ;
;
将参数方程代入椭圆方程![]() 可得:
可得:![]() ,
,
化简可得:![]() ,
,
若![]() ,则上面的方程为
,则上面的方程为![]() ,则
,则![]() ,矛盾
,矛盾
若![]() ,则
,则![]() ,
,![]() ,
,
则弦![]() 长为
长为![]()
![]()
![]()
![]() 上式
上式![]() ,
,
![]()
当且仅当![]() 即
即![]() 或
或![]() ,
,![]() 时等号成立.
时等号成立.
![]() 直线
直线![]() 方程为:
方程为:![]() 或
或![]()

练习册系列答案
相关题目