题目内容
若正方体的棱长为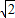 ,则以该正方体各个面的中心为顶点的凸多面体的体积为 .
,则以该正方体各个面的中心为顶点的凸多面体的体积为 .
【答案】分析:先求该正方体各个面的中心为顶点的凸多面体的底面棱长,求出它的高然后求出体积.
解答:解:所求八面体体积是两个底面边长为1,高为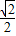 的四棱锥的体积和,
的四棱锥的体积和,
一个四棱锥体积V1= ×1×
×1×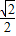 =
=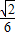 ,
,
故八面体体积V=2V1=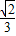 .
.
故答案为: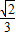
点评:本题考查棱柱的结构特征,几何体的内接体问题,考查空间想象能力,逻辑思维能力,是中档题.
解答:解:所求八面体体积是两个底面边长为1,高为
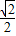 的四棱锥的体积和,
的四棱锥的体积和,一个四棱锥体积V1=
 ×1×
×1×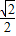 =
=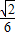 ,
,故八面体体积V=2V1=
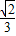 .
.故答案为:
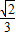
点评:本题考查棱柱的结构特征,几何体的内接体问题,考查空间想象能力,逻辑思维能力,是中档题.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目