Question

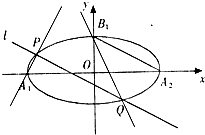如图，已知椭圆C：

x2

a2

+

y2

b2

=1(a＞b＞0)，A₁，A₂，B₁是椭圆C的顶点，若椭圆C的离心率e=

3

2

，且过点(

2

，

2

2

)．
（Ⅰ）求椭圆C的方程；
（Ⅱ）作直线l，使得l∥A₂B₁，且与椭圆C相交于P、Q两点（异于椭圆C的顶点），设直线A₁P和直线B₁Q的倾斜角分别是α，β，求证：α+β=π．

Answer 1

分析：（Ⅰ）利用椭圆的标准方程、离心率及其abc的关系即可得出；
（Ⅱ）把直线l的方程与椭圆的方程联立得到根与系数的关系、平行线之间的斜率关系、直线斜率的计算公式、两角和的正切公式即可得出．

解答：解：（Ⅰ）由已知得：

c a = 3 2 2 a2 + 1 2b2 =1 c2=a2-b2

，解得a=2，b=1，c=

3

．∴椭圆C的方程为

x2

4

+y2=1
（Ⅱ）由（Ⅰ）可知：A₁（-2，0），A₂（2，0），B₁（0，1）．
∴kA2B1=-

1

2

．
∵l∥A₁B₁，∴kl=kA2B1=-

1

2

．
可设直线l的方程为y=-

1

2

x+m，设P（x₁，y₁），Q（x₂，y₂）．
联立

y=- 1 2 x+m x2 4 +y2=1

消去y得x²-2mx+2m²-2=0．
∵直线l与椭圆有不同的两个交点，
∴△=4m²-4（2m²-2）＞0，即-

2

＜m＜

2

，
∴x1+x2=2m，x1x2=2m2-2．
∵P，Q异于椭圆C的顶点，∴α≠

π

2

，β≠

π

2

，∴tanα=kA1P=

y1

x1+2

，tanβ=kB1Q=

y2-1

x2

．
∴tanα+tanβ=

y1

x1+2

+

y2-1

x2

=

y1x2+x1y2+2y2-x1-2

x2(x1+2)

．
∵y1=-

1

2

x1+m，y2=-

1

2

x2+m．
∴tanα+tanβ=

(m-1)(x1+x2)-x1x2+2m-2

(x1+2)x2

=

2m(m-1)-(2m2-2)+2m-2

(x1+2)x2

=0，
∴tan(α+β)=

tanα+tanβ

1-tanαtanβ

=0．
又∵α，β∈（0，π），∴α+β∈（0，2π），故α+β=π．

点评：熟练掌握椭圆的标准方程及其性质、直线与椭圆相交问题的解法、根与系数的关系、平行线之间的斜率关系、直线斜率的计算公式、两角和的正切公式是解题的关键．