题目内容
在△ABC中,∠A=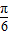 ,D是BC边上任意一点(D与B、C不重合),且丨
,D是BC边上任意一点(D与B、C不重合),且丨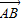 |2=
|2=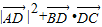 ,则∠B= .
,则∠B= .
【答案】分析:做高AE,不妨设E在CD上,设AE=h,CE=x,CD=p,BD=q,则DE=p-x,BE=p+q-x,根据勾股定理可分别表示出AD2和AB2,进而求得的表达式,根据题设等式可知pq=BD•CD,进而化简整理求得x=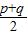 =
=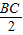 ,推断出ABC为等腰三角形.进而根据顶角求得B.
,推断出ABC为等腰三角形.进而根据顶角求得B.
解答:解:做高AE,不妨设E在CD上,设AE=h,CE=x,CD=p,BD=q,则DE=p-x,BE=p+q-x,
则AD2=AE2+DE2=h2+(p-x)2,
AB2=AE2+BE2=h2+(p+q-x)2,
AB2-AD2=(p+q-x)2-(p-x)2=q(q+2p-2x),
即pq=BD•CD=q(q+2p-2x),
q≠0,所以 p=q+2p-2x,
x=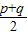 =
=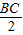 ,
,
即E为BC中点,于是ABC为等腰三角形.
顶角为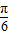 ,则底角B=
,则底角B=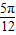
故答案为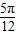 .
.
点评:本题主要考查了解三角形问题.解题的关键是通过题设条件建立数学模型,考查了学生分析问题和解决问题的能力.
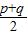 =
=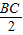 ,推断出ABC为等腰三角形.进而根据顶角求得B.
,推断出ABC为等腰三角形.进而根据顶角求得B.解答:解:做高AE,不妨设E在CD上,设AE=h,CE=x,CD=p,BD=q,则DE=p-x,BE=p+q-x,
则AD2=AE2+DE2=h2+(p-x)2,
AB2=AE2+BE2=h2+(p+q-x)2,
AB2-AD2=(p+q-x)2-(p-x)2=q(q+2p-2x),
即pq=BD•CD=q(q+2p-2x),
q≠0,所以 p=q+2p-2x,
x=
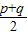 =
=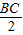 ,
,即E为BC中点,于是ABC为等腰三角形.
顶角为
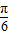 ,则底角B=
,则底角B=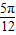
故答案为
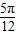 .
.点评:本题主要考查了解三角形问题.解题的关键是通过题设条件建立数学模型,考查了学生分析问题和解决问题的能力.

练习册系列答案
相关题目