题目内容
 长方体ABCD-A1B1C1D1中,底面ABCD是正方形,AA1=2,AB=1,E是DD1上的一点.
长方体ABCD-A1B1C1D1中,底面ABCD是正方形,AA1=2,AB=1,E是DD1上的一点.
(1)求异面直线AC与B1D所成的角;
(2)若B1D⊥平面ACE,求三棱锥A-CDE的体积.
解:以D为原点,DA、DC、DD1所在直线分别为x轴、y轴、z轴建立空间直角坐标系.
(1)依题意,D(0,0,0),A(1,0,0),C(0,1,0),B1(1,1,2),
∴ ,
,
∴ ,
,
∴异面直线AC与B1D所成的角为 .
.
(2)设E(0,0,a),则 ,
,
∵B1D⊥平面ACE,AE?平面ACE,∴B1D⊥AE.
∴ ,∴-1+2a=0,
,∴-1+2a=0, .
.
∴VA-CDE=VE-ADC= =
= .
.
分析:(1)建立如图所示的空间直角坐标系,利用异面直线的方向向量的夹角即可得到此两条异面直线所成的角;
(2)利用线面垂直的性质定理即可得到点E的坐标,利用VA-CDE=VE-ADC即可得到体积.
点评:熟练掌握通过建立空间直角坐标系的方法并利用异面直线的方向向量的夹角得到两条异面直线所成的角、及掌握线面垂直的性质定理、“等积变形”、三棱锥的体积计算公式是解题的关键.

(1)依题意,D(0,0,0),A(1,0,0),C(0,1,0),B1(1,1,2),
∴
 ,
,
∴
 ,
,∴异面直线AC与B1D所成的角为
 .
.(2)设E(0,0,a),则
 ,
,∵B1D⊥平面ACE,AE?平面ACE,∴B1D⊥AE.
∴
 ,∴-1+2a=0,
,∴-1+2a=0, .
.∴VA-CDE=VE-ADC=
 =
= .
.分析:(1)建立如图所示的空间直角坐标系,利用异面直线的方向向量的夹角即可得到此两条异面直线所成的角;
(2)利用线面垂直的性质定理即可得到点E的坐标,利用VA-CDE=VE-ADC即可得到体积.
点评:熟练掌握通过建立空间直角坐标系的方法并利用异面直线的方向向量的夹角得到两条异面直线所成的角、及掌握线面垂直的性质定理、“等积变形”、三棱锥的体积计算公式是解题的关键.

练习册系列答案
相关题目
长方体ABCD-A1B1C1D1中,AB=3,BC=4,AA1=5 则三棱锥A1-ABC的体积为( )
| A、10 | B、20 | C、30 | D、35 |
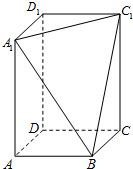 在长方体ABCD-A1B1C1D1中,AB=BC=2,过A1、C1、B三点的平面截去长方体的一个角后,得到如图所示的几何体ABCD-A1C1D1,且这个几何体的体积为10.
在长方体ABCD-A1B1C1D1中,AB=BC=2,过A1、C1、B三点的平面截去长方体的一个角后,得到如图所示的几何体ABCD-A1C1D1,且这个几何体的体积为10. 如图,长方体ABCD-A1B1C1D1中,AB=A1A=a,BC=
如图,长方体ABCD-A1B1C1D1中,AB=A1A=a,BC= 如图,已知多面体ABCD-A1B1C1D1,它是由一个长方体ABCD-A'B'C'D'切割而成,这个长方体的高为b,底面是边长为a的正方形,其中顶点A1,B1,C1,D1均为原长方体上底面A'B'C'D'各边的中点.
如图,已知多面体ABCD-A1B1C1D1,它是由一个长方体ABCD-A'B'C'D'切割而成,这个长方体的高为b,底面是边长为a的正方形,其中顶点A1,B1,C1,D1均为原长方体上底面A'B'C'D'各边的中点. 在长方体ABCD-A1B1C1D1中,AB=BC=1,AA1=2,E是侧棱BB1的中点.
在长方体ABCD-A1B1C1D1中,AB=BC=1,AA1=2,E是侧棱BB1的中点.