题目内容
设函数f(x)=|2x+1|-|x-2|.
(Ⅰ)求不等式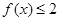 的解集;
的解集;
(Ⅱ)若{x|f(x)≥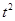 -t}∩{y|0≤y≤1}≠
-t}∩{y|0≤y≤1}≠ ,求实数t的取值范围.
,求实数t的取值范围.
(Ⅰ)解集为 ;(Ⅱ)
;(Ⅱ) .
.
解析试题分析:(Ⅰ)解不等式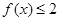 ,首先将
,首先将 转化为分段函数
转化为分段函数 ,然后利用分段函数分段解不等式,从而求出不等式的解;易错点,不知将
,然后利用分段函数分段解不等式,从而求出不等式的解;易错点,不知将 转化为分段函数;(Ⅱ)不等式
转化为分段函数;(Ⅱ)不等式 ,即
,即 在
在 时有解,只要
时有解,只要 在
在 的最大值大于
的最大值大于 即可,因此只需求出
即可,因此只需求出 在
在 的最大值即可, 而
的最大值即可, 而 ,易求出最大值,然后解一元二次不等式即可.
,易求出最大值,然后解一元二次不等式即可.
试题解析:(Ⅰ) ,所求解集为
,所求解集为
(Ⅱ)依题意得 在
在 时有解
时有解 ,
, ,
, ,则
,则
考点:本小题考查绝对值不等式的解法,考查学生数形结合的能力以及化归与转化思想,以及学生的运算能力.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目
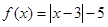 ,
,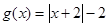 。
。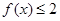 的解集;
的解集;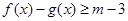 有解,求实数
有解,求实数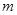 的取值范围。
的取值范围。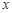 的不等式f(x)≥m2-3m的解集是R,求m的取值范围
的不等式f(x)≥m2-3m的解集是R,求m的取值范围 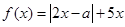 ,其中实数
,其中实数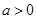 .
.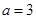 时,求不等式
时,求不等式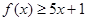 的解集;
的解集;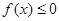 的解集为
的解集为 ,求
,求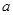 的值.
的值.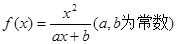 ,且方程
,且方程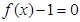 有两个实根为
有两个实根为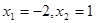 .
. 的解析式 ;
的解析式 ;  ,解关于x的不等式:
,解关于x的不等式: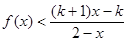 .
. 的不等式
的不等式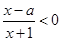 的解集为
的解集为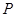 ,不等式
,不等式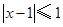 的解集为
的解集为 .
.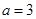 ,求
,求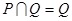 ,求正数
,求正数 的取值.
的取值.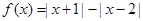 .
.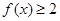 ;
;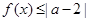 的解集为
的解集为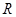 ,求实数
,求实数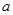 的取值范围.
的取值范围.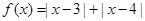 .
.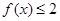 ;
;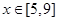 ,
,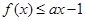 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围. .
.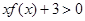 ;
;  ,不等式
,不等式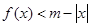 恒成立,求
恒成立,求 的取值范围.
的取值范围.