题目内容
定义在区间[0，1]上的函数f（x）满足：f（0）=f（1）=0，且对任意的x1，x2∈[0，1]都有f（
）≤f（x1）+f（x2）；
（1）证明：对任意的x∈[0，1]，都有f（x）≥0；
（2）求f（
）的值．
（1）任取x1=x2=x∈[0，1]，则f（
）≤f（x）+f（x），即f（x）≤2f（x），
∴f（x）≥0，
故对任意的x∈[0，1]都有f（x）≥0
（2）由f（0）=f（1）=0得f（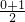
）≤f（0）+f（1）=0+0=0，
于是f（
）≤0，
又由（1）的结果知f（）≥0，
故f（）=0；
由f（）=0与f（1）=0
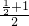得f（
）≤f（）+f（1）=0+0=0，
∴f（）≤0，又由（1）知f（）≥0，
故f（）=0．
分析：（1）任取x1=x2=x∈[0，1]，依题意，对任意的x1，x2∈[0，1]都有f（）≤f（x1）+f（x2），可证得f（x）≥0；
（2）利用f（0）=f（1）=0，结合已知可求得f（）≤0，而由（1）的结果知f（）≥0，从而可得故f（）=0；同理可求得f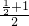（）=f（）的值．
点评：本题考查抽象函数及其应用，着重考查赋值法的灵活应用，考查推理分析与运算的能力，属于中档题．
）≤f（x）+f（x），即f（x）≤2f（x），∴f（x）≥0，
故对任意的x∈[0，1]都有f（x）≥0
（2）由f（0）=f（1）=0得f（
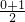）≤f（0）+f（1）=0+0=0，于是f（
）≤0，又由（1）的结果知f（
）≥0，故f（
）=0；由f（
）=0与f（1）=0得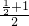f（
）≤f（）+f（1）=0+0=0，∴f（
）≤0，又由（1）知f（）≥0，故f（
）=0．分析：（1）任取x1=x2=x∈[0，1]，依题意，对任意的x1，x2∈[0，1]都有f（
）≤f（x1）+f（x2），可证得f（x）≥0；（2）利用f（0）=f（1）=0，结合已知可求得f（
）≤0，而由（1）的结果知f（）≥0，从而可得故f（）=0；同理可求得f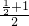（）=f（）的值．点评：本题考查抽象函数及其应用，着重考查赋值法的灵活应用，考查推理分析与运算的能力，属于中档题．
练习册系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
已知定义在区间[0，1]上的函数y=f（x）的图象如图所示，对于满足0＜x1＜x2＜1的任意x1、x2，给出下列结论：
已知定义在区间[0，1]上的函数y=f（x）的图象如图所示，对于满足0＜x1＜x2＜1的任意x1，x2，下列结论正确的是（ ）
| A、f（x2）-f（x1）＞x2-x1 | ||||
| B、f（x2）-f（x1）＜x2-x1 | ||||
C、
| ||||
| D、x2f（x1）＞x1f（x2） |
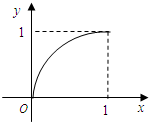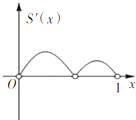
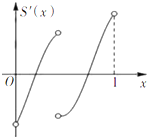
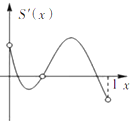
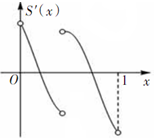
已知定义在区间[0，1]上的函数y=f（x）的图象如图所示，对于满足0＜x1＜x2＜1的任意x1，x2，给出下列结论：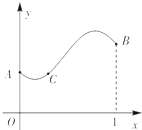
定义在区间[0，1]上的函数f（x）的图象如图所示，以A（0，f（0））、B（1，f（1））、C（x，f（x））为顶点的△ABC的面积记为函数S（x），则函数S（x）的导函数S′（x）的大致图象为（ ）
