题目内容
已知f(x)=xlnx,g(x)=-x2+ax-3(1)求函数f(x)在[t,t+2](t>0)上的最小值;
(2)对一切x∈(0,+∞),2f(x)≥g(x)恒成立,求实数a的取值范围;
(3)证明对一切x∈(0,+∞),都有lnx>
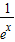 -
-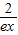 成立.
成立.
【答案】分析:(1)讨论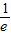 与区间[t,t+2](t>0)的关系,利用导数研究函数的单调性就看得出;
与区间[t,t+2](t>0)的关系,利用导数研究函数的单调性就看得出;
(2)对一切x∈(0,+∞),2f(x)≥g(x)恒成立,即-x2+ax-3≤2xlnx≤0,x∈(0,+∞).
?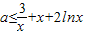 恒成立,x∈(0,+∞).?a≤
恒成立,x∈(0,+∞).?a≤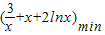 ,x∈(0,+∞).
,x∈(0,+∞).
利用导数求出其最小值即可.
(3)变形为:对一切x∈(0,+∞),都有lnx>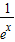 -
-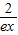 成立?
成立?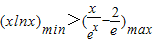 .利用导数分别求出即可.
.利用导数分别求出即可.
解答:解:(1)f′(x)=lnx+1,令f′(x)=0,解得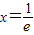 .∴f(x)在
.∴f(x)在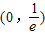 上单调递减,在
上单调递减,在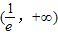 上单调递增.
上单调递增.
∵x∈[t,t+2](t>0),
①当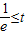 时,f(x)在[t,t+2](t>0)上单调递增,∴f(x)在x=t时取得最小值,f(t)=tlnt;
时,f(x)在[t,t+2](t>0)上单调递增,∴f(x)在x=t时取得最小值,f(t)=tlnt;
②当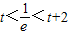 时,f(x)在x=
时,f(x)在x=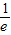 取得最小值,
取得最小值,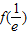 =
=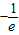 ;
;
(2)对一切x∈(0,+∞),2f(x)≥g(x)恒成立,即-x2+ax-3≤2xlnx≤0,x∈(0,+∞).
?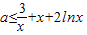 恒成立,x∈(0,+∞).?a≤
恒成立,x∈(0,+∞).?a≤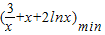 ,x∈(0,+∞).
,x∈(0,+∞).
令u(x)=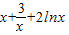 ,x∈(0,+∞).
,x∈(0,+∞).
则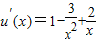 =
=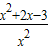 =
=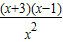 ,可知当且仅当x=1时,u(x)取得最小值,且u(1)=4.
,可知当且仅当x=1时,u(x)取得最小值,且u(1)=4.
∴a≤4.
(3)对一切x∈(0,+∞),都有lnx>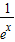 -
-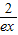 成立?
成立?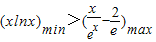 .
.
令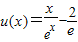 ,(x>0).
,(x>0).
∵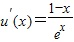 ,可知当且仅当x=1,u(x)取得最大值,且u(1)=
,可知当且仅当x=1,u(x)取得最大值,且u(1)=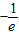 .
.
由(1)可知:(xlnx)min(x>0)=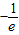 ,而
,而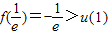 .
.
因此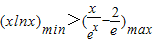 .
.
即对一切x∈(0,+∞),都有lnx>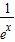 -
-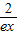 成立.
成立.
点评:熟练掌握利用导数研究函数的单调性极值与最值、分离参数法、等价转化等是解题的关键.
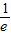 与区间[t,t+2](t>0)的关系,利用导数研究函数的单调性就看得出;
与区间[t,t+2](t>0)的关系,利用导数研究函数的单调性就看得出;(2)对一切x∈(0,+∞),2f(x)≥g(x)恒成立,即-x2+ax-3≤2xlnx≤0,x∈(0,+∞).
?
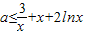 恒成立,x∈(0,+∞).?a≤
恒成立,x∈(0,+∞).?a≤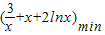 ,x∈(0,+∞).
,x∈(0,+∞).利用导数求出其最小值即可.
(3)变形为:对一切x∈(0,+∞),都有lnx>
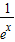 -
-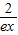 成立?
成立?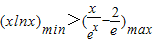 .利用导数分别求出即可.
.利用导数分别求出即可.解答:解:(1)f′(x)=lnx+1,令f′(x)=0,解得
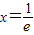 .∴f(x)在
.∴f(x)在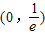 上单调递减,在
上单调递减,在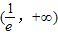 上单调递增.
上单调递增.∵x∈[t,t+2](t>0),
①当
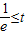 时,f(x)在[t,t+2](t>0)上单调递增,∴f(x)在x=t时取得最小值,f(t)=tlnt;
时,f(x)在[t,t+2](t>0)上单调递增,∴f(x)在x=t时取得最小值,f(t)=tlnt;②当
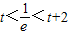 时,f(x)在x=
时,f(x)在x=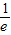 取得最小值,
取得最小值,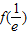 =
=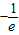 ;
;(2)对一切x∈(0,+∞),2f(x)≥g(x)恒成立,即-x2+ax-3≤2xlnx≤0,x∈(0,+∞).
?
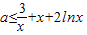 恒成立,x∈(0,+∞).?a≤
恒成立,x∈(0,+∞).?a≤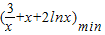 ,x∈(0,+∞).
,x∈(0,+∞).令u(x)=
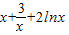 ,x∈(0,+∞).
,x∈(0,+∞).则
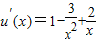 =
=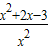 =
=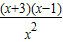 ,可知当且仅当x=1时,u(x)取得最小值,且u(1)=4.
,可知当且仅当x=1时,u(x)取得最小值,且u(1)=4.∴a≤4.
(3)对一切x∈(0,+∞),都有lnx>
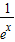 -
-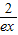 成立?
成立?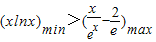 .
.令
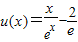 ,(x>0).
,(x>0).∵
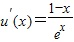 ,可知当且仅当x=1,u(x)取得最大值,且u(1)=
,可知当且仅当x=1,u(x)取得最大值,且u(1)=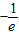 .
.由(1)可知:(xlnx)min(x>0)=
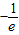 ,而
,而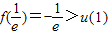 .
.因此
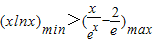 .
.即对一切x∈(0,+∞),都有lnx>
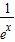 -
-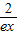 成立.
成立.点评:熟练掌握利用导数研究函数的单调性极值与最值、分离参数法、等价转化等是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目