题目内容
已知平面α⊥平面β,直线a∥α,a垂直于α与β的交线AB,试判断a与β的位置关系,并证明结论.
思路解析:利用线面垂直的判定可得.
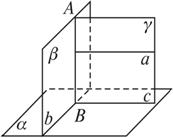
解:a与β的位置关系是直线a⊥平面β.
证明:过直线a作平面γ∩α=直线c,
∵a∥α,∴a∥c.
又∵a⊥AB,∴c⊥AB.
又∵c
α,α∩β=AB且α⊥β,∴c⊥β.
故a⊥β.
练习册系列答案
相关题目
题目内容
已知平面α⊥平面β,直线a∥α,a垂直于α与β的交线AB,试判断a与β的位置关系,并证明结论.
思路解析:利用线面垂直的判定可得.
解:a与β的位置关系是直线a⊥平面β.
证明:过直线a作平面γ∩α=直线c,
∵a∥α,∴a∥c.
又∵a⊥AB,∴c⊥AB.
又∵cα,α∩β=AB且α⊥β,∴c⊥β.
故a⊥β.
16、如图：已知平面α∥平面β，点A、B在平面α内，点C、D在β内，直线AB与CD是异面直线，点E、F、G、H分别是线段AC、BC、BD、AD的中点，求证：
//平面
,点A、B在平面