题目内容
【题目】已知函数f（x）= 
+log2x．
（1）求f（2），f（ 
），f（4），f（ 
）的值，并计算f（2）+f（ ），f（4）+f（ ）；
（2）求f（1）+f（2）+f（3）+…+f（2016）+f（ ）+f（ 
）+…f（ 
）的值．
【答案】
（1）解：∵f（x）= 
+log2x，
∴f（2）= 
= 
，
f（ 
）= 
，
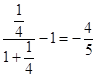f（4）=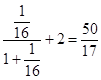 
，
f（ 
）= 
，
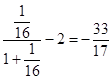∴f（2）+f（ ）=1，f（4）+f（ ）=1
（2）解：∵f（x）+f（ 
）= + 
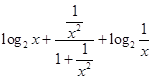=1，
∴f（1）+f（2）+f（3）+…+f（2016）+f（ ）+f（ 
）+…f（ 
）
=f（1）+[f（2）+f（ ）]+[f（3）+f（ ）]+…+[f（2016）+f（ ）]
= 
= 
【解析】（1）由f（x）= +log2x，能求出f（2），f（ ），f（4），f（ ），f（2）+f（ ），f（4）+f（ ）的值．（2）由f（x）+f（ ）=1，能求出f（1）+f（2）+f（3）+…+f（2016）+f（ ）+f（ ）+…f（ ）的值．
【考点精析】解答此题的关键在于理解函数的值的相关知识，掌握函数值的求法：①配方法(二次或四次)；②“判别式法”；③反函数法；④换元法；⑤不等式法；⑥函数的单调性法．
练习册系列答案
举一反三同步巧讲精练系列答案
口算与应用题卡系列答案
相关题目
