题目内容
已知双曲线C：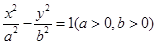
的离心率为
，左顶点为（-1，0）。
（1）求双曲线方程；
（2）已知直线x-y+m=0与双曲线C交于不同的两点A、B，且线段AB的中点在圆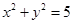
上，求m的值和线段AB的长。
（1）
（2）
解析试题分析：（1）因为双曲线的离心率为，所以
，又左顶点为
，所以
，因此可解得
，
，从而求得双曲线的标准方程：
（2）设
，
中点
的坐标为
，则
联立方程组：
消去
得关于
的一元二次方程，在判别式大于零的条件下，由韦达定理可用含参数
的表达式表示
和
，进而表示
和
，由于点到原点的距离为
，可据此列方程解得的值；最后根据弦长公式求弦的长.
试题解析：
（1）依题意
所以
..2分
所以双曲线方程为 ..4分
（2）由得
， .6分
∴
，
又∵中点在直线
上，所以可得中点坐标为（m,2m）,
代入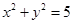得
.8分
|AB|=
。 12分
考点：1、双曲线的标准方程；2、直线与双曲线的位置关系；2、弦长公式.
练习册系列答案
相关题目
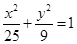，直线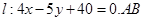
是直线上的线段，且
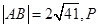是椭圆上一点，求
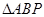面积的最小值。
-
=1(a>0,b>0)上一点,M,N分别是双曲线E的左,右顶点,直线PM,PN的斜率之积为
.
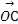=λ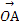
+
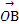,求λ的值.
.
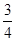.过F1的直线交椭圆C于A，B两点，且△ABF2的周长为8.过定点M(0，3)的直线l1与椭圆C交于G，H两点(点G在点M，H之间)．
＋
＝1(a>b>0)过点(0,4)，离心率为
.
的直线被C所截线段的中点坐标．
的中心在坐标原点O，左顶点
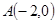，离心率
，
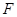为右焦点，过焦点
、
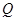两点（不同于点
）．
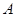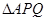的面积
时，求直线PQ的方程；
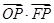的范围．