题目内容
直线y=kx交双曲线C：
-
=1于A，B两点，P为双曲线C上异于A，B的任意一点，则直线PA，PB的斜率之积为（ ）
| x2 |
| 4 |
| y2 |
| 3 |
分析：设出P，A，B的坐标，代入双曲线方程，进而表示出直线PA、PB的斜率之积，化简即可得出结论．
解答：解：设P（x，y），A（m，km），则B（-m，-km），代入双曲线方程可得
-
=1，
∴(km)2=
-3，
∵双曲线C：
-
=1，
∴y2=
-3，
∴直线PA、PB的斜率之积为
•
=
=
=
．
故选B．
| m2 |
| 4 |
| (km)2 |
| 3 |
∴(km)2=
| 3m2 |
| 4 |
∵双曲线C：
| x2 |
| 4 |
| y2 |
| 3 |
∴y2=
| 3x2 |
| 4 |
∴直线PA、PB的斜率之积为
| y-km |
| x-m |
| y+km |
| x+m |
| y2-(km)2 |
| x2-m2 |
| ||||
| x2-m2 |
| 3 |
| 4 |
故选B．
点评：本题考查双曲线的标准方程，考查直线的斜率，考查学生的计算能力，属于中档题．
练习册系列答案
灵星计算小达人系列答案
孟建平错题本系列答案
相关题目
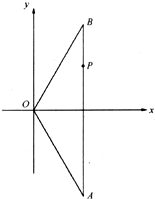（2006•广州一模）如下图，在△OAB中，|OA|=|OB|=4，点P分线段AB所成的比为3：1，以OA、OB所在直线为渐近线的双曲线M恰好经过点P，且离心率为2．