题目内容
已知函数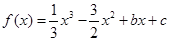 ,且
,且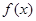 在
在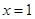 处取得极值.
处取得极值.
(1)求 的值;
的值;
(2)若当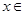 [-1,
[-1,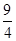 ]时,
]时,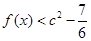 恒成立,求
恒成立,求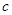 的取值范围.
的取值范围.
【答案】
(1)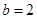
(2)(-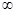 ,-1)
,-1)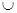 (2,+
(2,+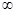 )
)
【解析】(1)因为 ,
,
所以 .……………………………………………2分
.……………………………………………2分
因为 在
在 处取得极值,
处取得极值,
所以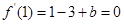 .…………………………………………4分
.…………………………………………4分
解得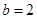 .……………………………………………………5分
.……………………………………………………5分
(2)因为 .
.
所以
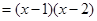 ,……………………………………………………6分
,……………………………………………………6分
当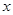 变化时,
变化时,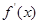 ,
, 的变化情况如下表:
的变化情况如下表:
|
|
-1 |
|
1 |
|
2 |
|
|
|
|
|
|
0 |
|
0 |
|
|
|
|
|
单调递增 |
|
|
|
单调递增 |
|
因此当 时,
时, 有极大值
有极大值 .…………………………………8分
.…………………………………8分
又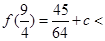
 ,
,

 ,
,
∴ [-1,
[-1, 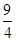 ]时,
]时, 最大值为
最大值为 .………………10分
.………………10分
∴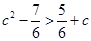 .
……………………………………………………12分
.
……………………………………………………12分
∴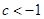 或
或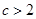 .
.
∴ 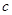 的取值范围为(-
的取值范围为(-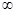 ,-1)
,-1)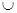 (2,+
(2,+ )……………………………14分
)……………………………14分

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目







 单调递减
单调递减


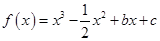 ,且
,且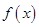 在
在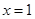 处取得极值.
处取得极值.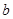 的值;
的值; 时,
时,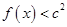 恒成立,求
恒成立,求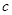 的取值范围;
的取值范围;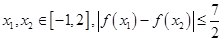 是否恒成立?如果成立,给出证明,如果不成立,请说明理由.
是否恒成立?如果成立,给出证明,如果不成立,请说明理由. 是定义在
是定义在 上的奇函数,且
上的奇函数,且 在
在 处取得极小值
处取得极小值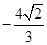 。设
。设 表示
表示 满足:
满足:
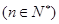
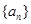 的通项公式
的通项公式 ;
;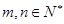 ,若
,若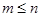 ,证明:
,证明: ;
;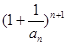 与
与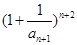 的大小。
的大小。 为奇函数,且
为奇函数,且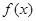 在
在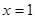 处取得极大值2.
处取得极大值2.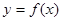 的解析式;
的解析式;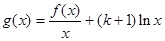 ,求函数
,求函数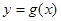 的单调区间。
的单调区间。